Вычисление площадей: Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс

Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №24. Вычисление площадей с помощью интегралов.

Перечень вопросов, рассматриваемых в теме

1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.

: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

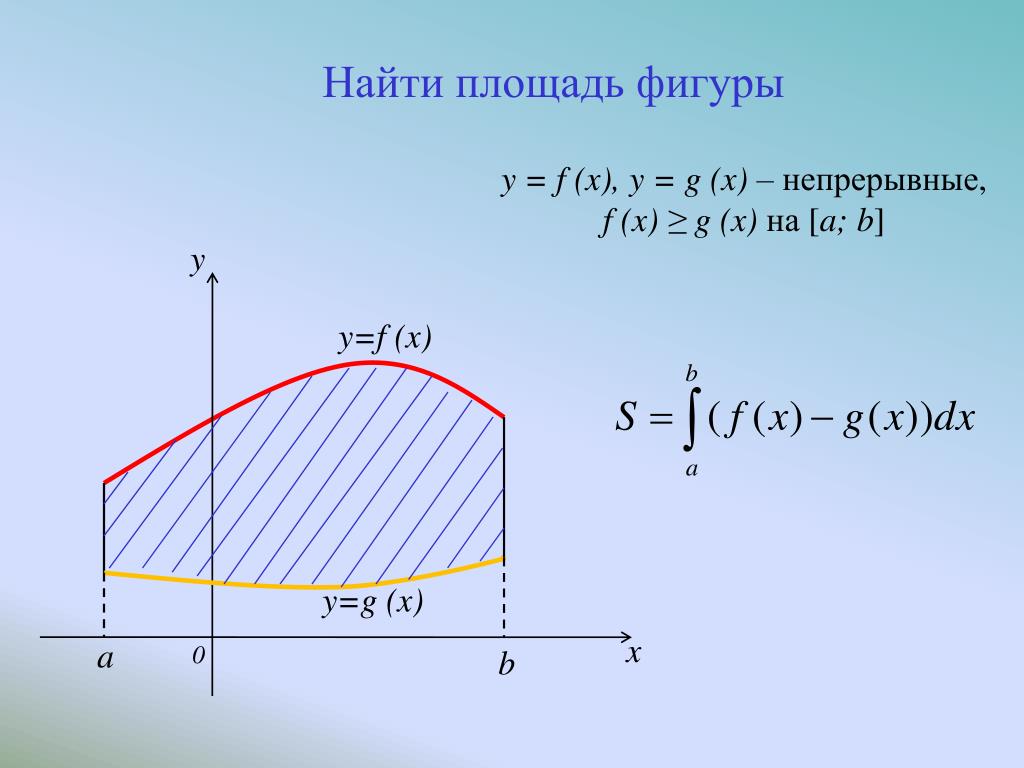
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)

Примеры и разбор решения заданий тренировочного модуля

№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.

Решение. Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).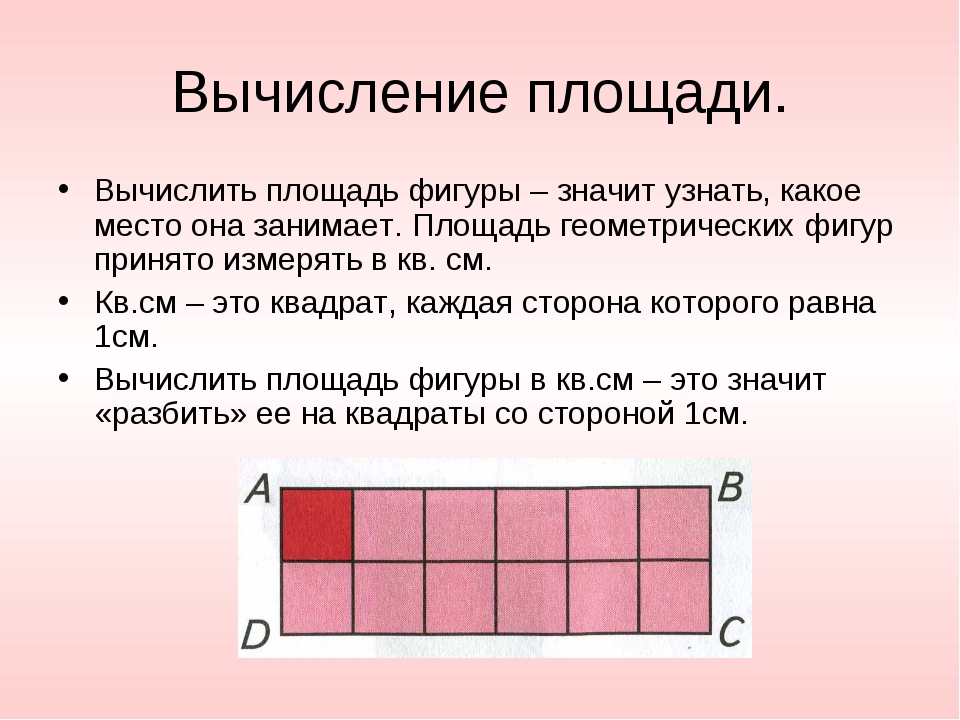

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а)    , это и будет ответ

№2. Найти площадь фигуры, ограниченной линиями у=4-х²,у=3х, у=0 и находящейся в 1-й четверти.

Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b)  .

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а)    , это и будет ответ.

Решение. S=S_OAB +S_ABC

№3. Найти площадь криволинейной трапеции (х-1)², ограниченной линиями х=2 и х=1, осью 0х

Решение:

Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию  F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b)  .

Затем подставляем значение нижнего предела в первообразную функцию: F(а) .

Рассчитываем разность F(b)  — F(а), это и будет ответ.

Math.ru

Абрам Миронович Лопшиц

Гостехиздат, 1956. 60 с.
Тираж 40000 экз.
Серия Популярные лекции по математике, выпуск 20

Загрузить (Mb) djvu (0.43) pdf (-) ps (-) html (-) tex (-)

Эта книжка познакомит читателя с понятием площади ориентированной фигуры и его применениями к теории планиметра и к выводу целесообразной формулы для вычисления площади участка, заданного на местности и ограниченного произвольной замкнутой ломаной линией. Понятие ориентированной площади может быть использовано, как в этом убедится читатель, и для решения задач школьной геометрии.

В основу книжки положен материал лекций, читанных мной школьникам старших классов.

А. Лопшиц

---

Содержание

Предисловие

Введение

Глава I. Измерение площади ориентированной фигуры

&nbsp&nbsp&nbsp§ 1. Ориентированный треугольник

&nbsp&nbsp&nbsp§ 2. Ориентированная площадь ориентированного треугольника

&nbsp&nbsp&nbsp§ 3. Теорема сложения

&nbsp&nbsp&nbsp§ 4. Строгое доказательство теоремы сложения

&nbsp&nbsp&nbsp§ 5. Ориентированный многоугольник

&nbsp&nbsp&nbsp§ 6. Площадь ориентированного многоугольника

&nbsp&nbsp&nbsp§ 7. Несколько примеров и задач

Глава II. Планиметр

&nbsp&nbsp&nbsp§ 1. Полярный планиметр

&nbsp&nbsp&nbsp§ 2.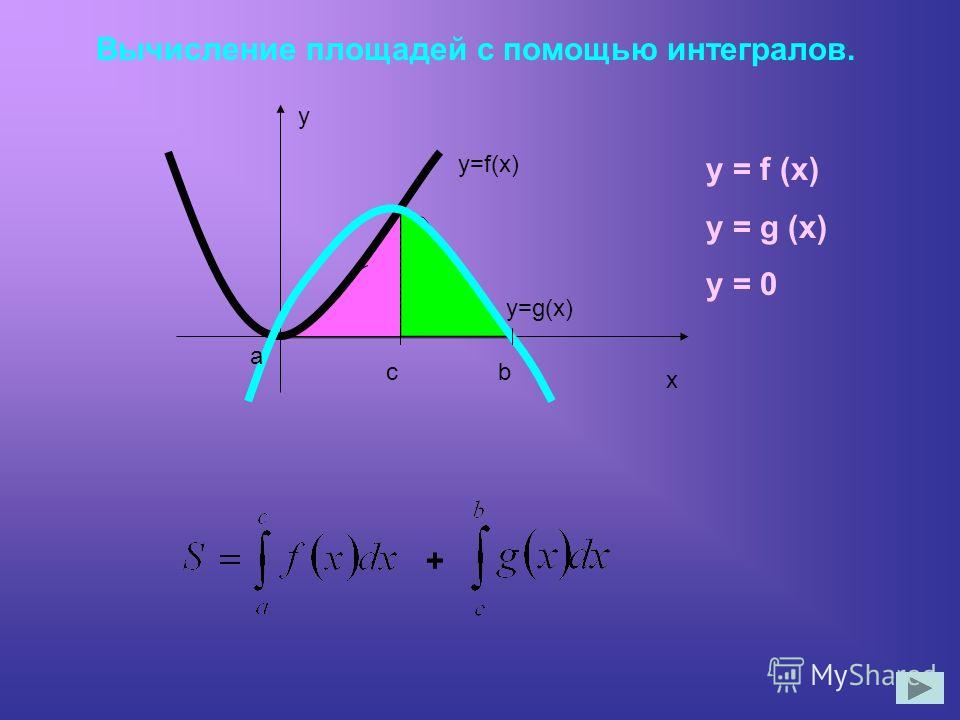 Прямолинейный планиметр

&nbsp&nbsp&nbsp§ 3. Элементарное перемещение рычага планиметра

&nbsp&nbsp&nbsp§ 4. Число оборотов счетного колеса при элементарном перемещении рычага

&nbsp&nbsp&nbsp§ 5. Число оборотов счетного колеса при замкнутом перемещении рычага

&nbsp&nbsp&nbsp§ 6. Вспомогательная геометрическая теорема

&nbsp&nbsp&nbsp§ 7. Использование вспомогательной геометрической теоремы для теории планиметра

Глава III. Вычисление площади многоугольника, заданного на местности

&nbsp&nbsp&nbsp§ 1. Постановка задачи

&nbsp&nbsp&nbsp§ 2. Несколько определений и обозначений

&nbsp&nbsp&nbsp§ 3. Вспомогательная теорема

&nbsp&nbsp&nbsp§ 4. Формула для вычисления площади ориентированного многоугольника

&nbsp&nbsp&nbsp§ 5. Вычисление ориентированных углов

&nbsp&nbsp&nbsp§ 6. Вычисление углов между несмежными сторонами ориентированного многоугольника

&nbsp&nbsp&nbsp§ 7. Тригонометрическая формула для вычисления площади ориентированного многоугольника

&nbsp&nbsp&nbsp§ 8. Теоретическое использование формулы, выведенной для практических целей

---

Загрузить (Mb) djvu (0.43) pdf (-) ps (-) html (-) tex (-)

Постоянный адрес этой страницы: http://math.ru/lib/plm/20

Вычисление площадей и объемов с помощью двойных интегралов.

Площадь области.

Площадь области $S,$ расположенной в плоскости $O_{xy}$ вычисляется по формуле $$S=\iint\limits_{S}dxdy.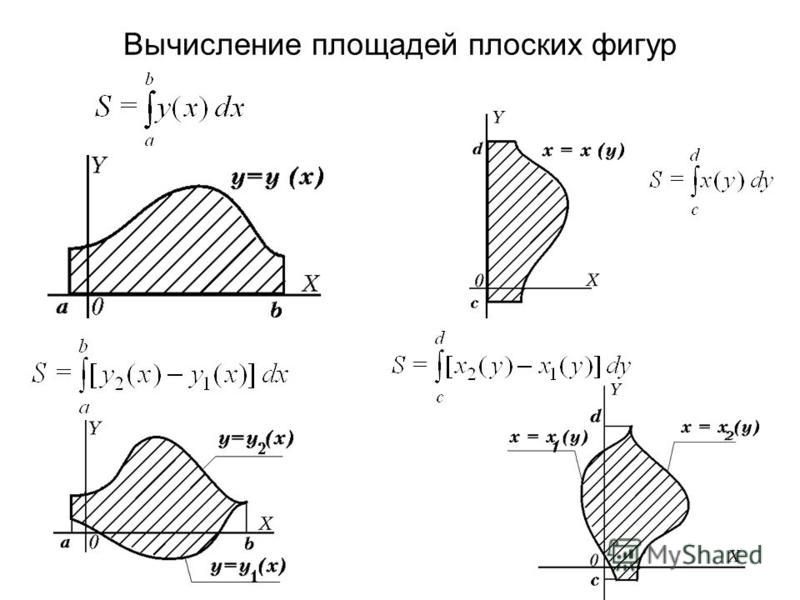 4dv=2. $$

 

Объём цилиндроида.

Объём цилиндроида, ограниченного сверху непрерывной поверхностью $z=f(x, y)\geq 0,$ снизу плоскостью $z=0$ и с боков прямой цилиндрической поверхностью, вырезающей из плоскости $O_{xy}$ квадрируемую область $\Omega$ равен $$V=\iint\limits_{\Omega}f(x, y)dxdy.$$ 

 

Вычисление площадей в прямоугольных координатах.

 |   |   |   |   |   |  Вычисление площадей в прямоугольных координатах.  |   |   |   |   |   | 

Если на отрезке   функция , то, площадь криволинейной трапеции, ограниченной кривой y=f(x), осью ОХ и прямыми x=a и x=b равна

 

если  на , то площадь криволинейной трапеции

В общем виде можно формулу для нахождения площади криволинейной трапеции записать в виде:

Примеры:

Пример1:

Сделаем чертёж фигуры, ограниченной указанными линиями:

 

Найдём площадь фигуры с помощью определённого интеграла:

Ответ: кв.

ед.

 

 

Если необходимо вычислить площадь, ограниченную кривыми    и и прямыми  x=a и x=b, то при условии   будем иметь

Пример:

 

Найти площадь фигуры, ограниченной данными линиями:

, .

Сделать чертеж.

Решение.

Найдем точки пересечения данных кривых. Для этого решим систему уравнений:

                                                   .

            Решаем полученное уравнение. Получаем

                                                                 ,   .

            Таким образом, точки пересечения кривых имеют координаты:  и .

Построим данную фигуру (рис.1).

 

Площадь данной фигуры находим по формуле :

                                .

Применяем формулу Ньютона-Лейбница

         .       

            

Ответ:  (кв. ед.).

 

Задачи для ОГЭ. Вычисление площадей

Задачи для ОГЭ с ответами и решениями

Вычисление площадей I

 

перейти к содержанию задачника

1. Найдите диагональ квадрата, если его площадь равна 4,5.
2. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 0,5 и 2.
3. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 13 и 52.
4. Найдите площадь параллелограмма, если две его стороны равны 40 и 10,  угол между ними равен 30^o.
5. Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150^o.
6. Найдите площадь ромба, если его стороны равны 5, а один из углов равен 150^o.
7. Площадь прямоугольного треугольника равна 224. Один из его катетов равен 28. Найдите другой катет.
8. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150^o. Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.
9. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150^o. Боковая сторона треугольника равна 34. Найдите площадь этого треугольника.
10. Найдите площадь треугольника, две стороны которого равны 44 и 8, а угол между ними равен 30^o.
11. Площадь треугольника АВС равна 12. DE — средняя линия. Найдите площадь треугольника CDE.
12. Площадь треугольника АВС равна 70. DE — средняя линия. Найдите площадь треугольника CDE.
13. Основания трапеции равны 8 и 2, высота равна 4. Найдите площадь трапеции
14. Основания трапеции равны 24 и 18, высота равна 4. Найдите площадь трапеции
15. Периметры двух подобных многоугольников относятся как 1 : 10. Площадь меньшего многоугольника равна 9. Найдите площадь большего многоугольника.
16. Периметры двух подобных многоугольников относятся как 1 : 3. Площадь меньшего многоугольника равна 3. Найдите площадь большего многоугольника.
17. Площадь круга равна . Найдите длину его окружности.
18. Площадь круга равна . Найдите длину его окружности.
19. Найдите площадь сектора круга радиуса , центральный угол которого равен 90^o.
20. Найдите площадь сектора круга радиуса 16, длина дуги которого равна 1.
21. Найдите площадь прямоугольника, если его периметр равен 20 и одна сторона на 8 больше другой.
22. Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 3 : 10.
23. Найдите периметр прямоугольника, если его площадь равна 624, а отношение соседних сторон равно 4 : 39.
24. Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
25. Сторона прямоугольника относится к его диагонали как 15 : 17, а другая сторона равна 16. Найдите площадь прямоугольника.
26. Стороны параллелограмма равны 44 и 88. Высота, опущенная на первую сторону, равна 66. Найдите высоту, опущенную на вторую сторону параллелограмма.
27. Стороны параллелограмма равны 10 и 85. Высота, опущенная на первую сторону, равна 51. Найдите высоту, опущенную на вторую сторону параллелограмма.
28. Найдите площадь ромба, если его высота равна 5, а острый угол равен 30^o.
29. Найдите площадь ромба, если его диагонали равны 13 и 6.
30. Найдите площадь ромба, если его диагонали равны 315 и 2.
31. Площадь ромба равна 507. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.
32. Площадь прямоугольного треугольника равна 65. Один из его катетов на 3 больше другого. Найдите меньший катет.

перейти к содержанию задачника

Ответы

1. 3
2. 1
3. 26
4. 200
5. 18
6. 12,5
7. 16
8. 1
9. 289
10. 88
11. 3
12. 17,5
13. 20
14. 84
15. 900
16. 27
17. 10
18. 22
19. 25
20. 8
21. 9
22. 120
23. 172
24. 14,5
25. 480
26. 33
27. 6
28. 50
29. 39
30. 315
31. 13
32. 10

 

Метки ОГЭ. Смотреть запись.

Вычисление площади фигуры в полярных координатах

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y=f(x), x=g(y) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Краткий обзор статьи

• Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
• Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
• В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Полярная система координат и криволинейный сектор

Определение 1

Точка, расположенная в полярной системе координат, имеет полярный угол φ0 и полярный радиус r0≥0. Полярный угол φ0 отсчитывается от полярной оси по часовой стрелке, а r0 — это расстояние от заданной точки до начала координат.

На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ0=3π4 и расстоянием до полюса r0=4.

Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью. 

Задать связь полярных и декартовых координат можно соотношениями r=x2+y2φ=arctgyx, x≠0 и обратно x=r·cosφy=r·sinφ.

Координаты красной точки на чертеже 23; 2. Положение этой точки задается углом φ0=arctg223=π6 и расстоянием r0=232+22=4.

В полярной системе координат равенство φ=α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ=0. Равенство r=C>0 задает окружность с центром в начале координат, где  — это радиус.

Функция r=p(φ), φ∈α; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r=p(φ), φ∈α; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ=φ0∈α; β. Однако мы будем встречать и отрицательные значенияr=p(φ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

На рисунке мы изобразили несколько примеров линий в полярной системе координат.

Дадим определение криволинейному сектору.

Определение 2

Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ=α, φ=β и некоторой линией  r=p(φ)≥0, непрерывной на участке α; β.

На рисунке мы привели несколько примеров криволинейных секторов.

На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ=-π6, φ=π6, которые не являются ее границами.

Площадь криволинейного сектора — вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: Sкругового сектора=γ·R22. Задаем внутренний угол γ в радианах.

Разобьем криволинейный сектор на n частей такими лучами 

φ=φ1, φ=φ2,…, φ=φn-1, что α=φ0<φ1<φ2<…<φn-1<β и λ=maxi=1, 2,…, nφi-φi-1→0 при n→+∞.

Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S(G) как сумму площадей секторов S(Gi) на каждом из участков разбиения:

S(G)=∑i=1nS(Gi)

Обозначим наибольшее и наименьшее значения функции r=p(φ) на i-ом отрезке φi-1; φi, i=1, 2,…, n как Rmini и Rmaxi . На каждом из отрезков построим по два круговых сектора Pi и Qi с максимальным и минимальным радиусами Rmini и Rmaxi соответственно.

Фигуры, которые являются объединением круговых секторов Qi, i=1, 2,…, n; Pi, i=1, 2,…, n , обозначим как P и Q соответственно.

Их площади будут равны S(P)=∑i=1nS(Pi)=∑i=1n12(Rmini)2·φi-φi-1 и S(Q)=∑i=1nS(Qi)=∑i=1n12(Rmaxi)2·φi-φi-1, причем S(P)≤S(G)≤S(Q).

Так как функция r=pφ непрерывна на отрезке α; β, то функция 12p2φ будет непрерывна на этом отрезке. Если рассматривать S(P) и S(Q) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

limλ→0S(P)=limλ→0S(Q)=S(G)⇒S(G)=limλ→0∑ i=1n12(Rmini)2·φi-φi-1==limλ→0∑ i=1n12(Rmaxi)·φi-φi-1=12∫βαp2φdφ

Определение 3

Формула для определения площади криволинейного сектора имеет вид:

S(G)=12∫βαp2φdφ

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

Пример 1

Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r=2sin2φи лучами φ=π6, φ=π3.

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r=2sin(2φ)положительна и непрерывна на отрезке φ∈π6, π3.

Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S(G)=12∫π6π3(2sin(2φ)2dφ=∫π6π32(sin(2φ)2dφ=∫π6π32·1-cos4φ2dφ=∫π6π3(1-cos(4φ))dφ=φ-14sin(4φ)π6π3==π3-14sin4π3-π6-14sin4π6=π6+34

Ответ: S(G)=π6+34

Задача упрощается в тех случаях, когда лучи φ=φ1, φ=φ2, ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r=p(φ). В этих случаях применить формулу S(G)=12∫αβp2(φ)dφ сразу не получится. Для начала придется решить неравенство p(φ)≥0  для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r=pφ неотрицательная. В противном случае нам придется ориентироваться  только на область определения и период функции.

Пример 2

Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r=-3·cos3φ.

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство -3·cos3φ≥0:

-3·cos3φ≥0⇔cos3φ≤0⇔cos φ≤0⇔⇔π2+2πk≤φ≤3π2+2πk, k∈Z

Построим функцию в полярных координатах на отрезке φ∈π2; 3π2 (при k=0). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π2+2πk и 3π2+2πk соответственно для любого целого значения k.

S(G)=12∫π23π2(-3·cos3φ)dφ=92∫π23π2cos6φdφ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида Kn(x)=sin x·cosn-1(x)n+n-1nKn-2(x), где Kn(x)=∫cosn(x)dx.

∫cos6φdφ=sin φ·cos5φ6+56∫cos4φdφ==sin φ·cos5φ6+56sin φ·cos3φ4+34cos2φdφ==sin φ·cos5φ6+5sin φ·cos3φ24+1524sin φ·cos φ2+12∫cos0φdφ==∫π23π2cos6φdφ=sin φ·cos5φ6+5sin φ·cos3φ24+15sin φ·cos φ48+15φ48π23π2==1548·3π2-1548·π2=5π16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S(G)=92∫π23π2cos6φdφ=92·5π16=45π32.

Ответ: S(G)=45π32

В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы.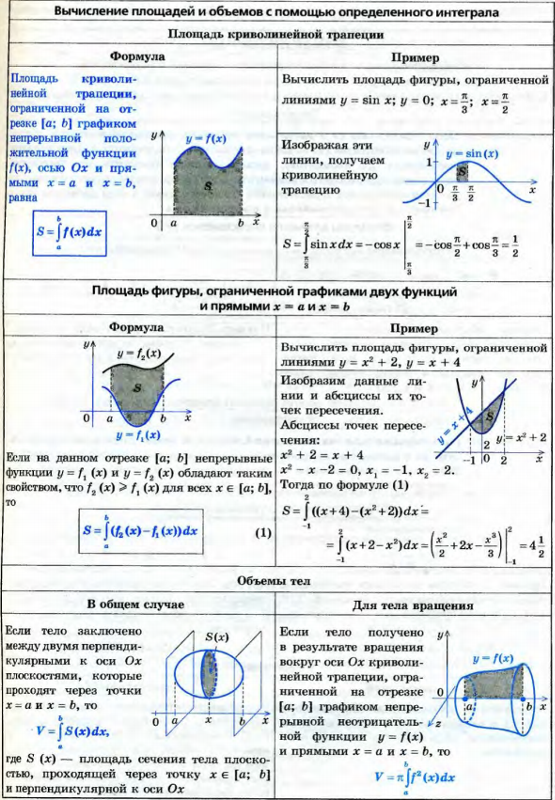 В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

Пример 3

Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r=3·cos(3φ).

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos(3φ)≥0⇔-π2+2πk≤3φ≤π2+2πk, k∈Z-π6+2π3k≤φ≤π6+2π3k, k∈Z

Таким образом, период функции r=3·cos3φ равен 2π3. Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

Вычислим площадь одного участка, расположенного на интервале φ∈π2; 5π6(при k=1):

12∫π25π69cos(3φ)dφ=12·3sin(3φ)π25π6=32sin3·5π6-sin3·π2=32(1-(-1)=3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

Площадь фигуры, которую ограничивает лемниската Бернулли

Определение 4

Лемниската Бернулли задается уравнением r=α·cos2φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при -π4+π·k≤φ≤π4+π·k, k∈Z.

Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S(G)=2·12∫-π4π4a2cos(2φ)2φ=a22(sin(2φ))-π4π4==a22sin2·π4-sin2·-π4=a2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a.

Площадь фигуры, границей которой является кардиоида

В полярной системе координат кардиоида задается уравнением вида r=2a(1+cosφ). В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2π. Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число,  а верхним, то, которое на 2π больше нижнего.

Вычислим площадь фигуры, ограниченной кардиоидой r=2a(1+cosφ), для φ∈0; 2π:

S(G)=12∫02π(2a(1+cosφ))2dφ=2a2∫02π(1+2cosφ+cos2φ)dφ==2a2∫02π1+2cosφ+1+cos2φ2dφ==2a2∫02π32+2cosφ+cos(2φ)2dφ==2a232φ+2sin φ+14sin2φ02π=6π·a2

Площадь фигуры, которую ограничивает улитка Паскаля

В полярной системе координат улитка Паскаля может быть задана уравнением r=b+2a·cosφ. В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при  b=2a.

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда  функцию r неотрицательная.

При b<-2a функция r=b+2a·cosφ будет отрицательной для любого значения угла φ.

При b=-2a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При -2a< b< 0 функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z.

При 0<b<2a функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z. Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

При b>2a функция r=b+2a·cosφ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b.

Пример 4

Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r=-3+6cosφ и r=5+4cosφ в полярной системе координат.

Решение

Формула r=-3+6cosφ соответствует фигуре, известной как улитка Паскаля..

Функция r=-3+6cosφ определена для всех значений угла φ. Нам необходимо выяснить, при каких φ функция будет неотрицательной:

-3+6cosφ≥0⇔cosφ≥12⇔-π3+2πk≤φ≤π3+2πk, k∈Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля: 

S(G)=12∫-π3π3(-3+6cosφ)2dφ=92∫-π3π3(1-4cosφ+4cos2φ)dφ==92∫-π3π31-4cosφ+4·1+cos2φ2dφ==92∫-π3π3(3-4cosφ+2cos(2φ))dφ=92·3φ-4sinφ+sin(2φ-π3π3==92·3·π3-4sinπ3+sin2π3-3·-π3-4sin-π3+sin-2π3==92·2π-33

Улитка Паскаля, определяемая формулой r=5+4cosφ, соответствует пятому пункту. Функция r=5+4cosφ определена и положительна для всех действительных значений φ. Поэтому, площадь фигуры в этом случае равна:

S(G)=12∫02π(5+4cosφ)2dφ=12∫02π(25+40cosφ+16cos2φ)dφ==12∫02π25+40cosφ+16·1+cos(2φ)2dφ==12∫02π(33+40cosφ+8cos(2φ))dφ=12·33φ+40sinφ+4sin(2φ02π==12·33·2π+40sin(2π+4sin(4π)-33·0+40sin 0+4sin 0=33π

Ответ: S(G)=33π

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Пример 5

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r=αφ, α>0, а вторая первым витком логарифмической спирали r=αφ, α>1.

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

Исходя из этого, найдем площадь фигуры по формуле:

S(G)=12∫02π(αφ)2dϕ=α22∫02πφ2dφ=α22·φ3302π=4α3π33

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S(G)=12∫02π(αϕ)2dϕ=12∫02πa2φdφ=14ln a·a2φ02π==14ln a·a4π-1

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ=α, φ=β и непрерывными и неотрицательными на интервале φ∈α; β функциями r=p1(φ) и r=p2(φ), причем p1(φ)≤p2(φ) для любого угла φ=φ0∈α; β.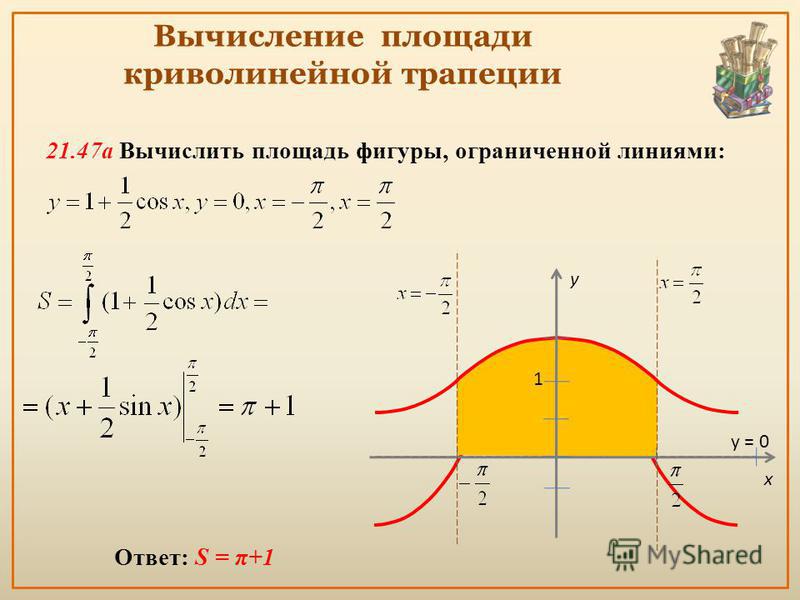

Находим площадь фигуры по формуле S(G)=12∫αβp22(φ)-p12(φ)dφ.

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G2 и G1.

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S(G)=S(G2)-S(G1)=12∫αβp22(φ)dφ-12∫αβp12(φ)dφ==12∫αβp22(φ)-p12(φ)dφ

Последний переход возможен в силу третьего свойства определенного интеграла.

Пример 6

Необходимо вычислить площадь фигуры, которая ограничена линиями φ=0, φ=π3, r=32, r=12φв полярной системе координат.

Решение

Построим заданную фигуру на графике.

Очевидно, что r=32 больше r=12φ для любого φ∈0; π3. Применяем полученную формулу для вычисления площади фигуры:

S(G)=12∫0π3322-12φ2dφ=12∫0π394-2-2φdφ==12·94φ+12·2-2φln 20π3=12·94φ+1ln 2·122φ+10π3==12·94·π3+1ln 2·122·π3+1-94·0+1ln 2·122·0+1==12·3π4+2-2π3-12·ln 2

Ответ: S(G)=12·3π4+2-2π3-12·ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

Пример 7

Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y=13x, x=3x, окружностями (x-2)2+(y-3)2=13, (x-4)2+(y-3)2=25.

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x=r·cosφy=r·sinφ⇒y=13x⇔r·sinφ=r·cosφ3⇔tgφ=13⇔φ=π6+πky=3x⇔r·sinφ=3·r·cosφ⇔tgφ=3⇔φ=π3+πk(x-2)2+(y-3)2=13⇔x2+y2=4x+6y⇔r=4cosφ+6sinφ(x-4)2+(y-3)2=25⇔x2+y2=8x+6y⇔r=8cosφ+6sinφ

Функция r=8cosφ+6sinφ больше r=4cosφ+6sinφ для любого φ∈π6; π3. Вычисляем площадь фигуры в полярных координатах:

S(G)=12∫π6π38cosφ+6sinφ2-4cosφ+6sinφ2dφ==12∫π6π3(48cos2φ+48cosφ·sinφ)dφ==24∫π6π3cos2φdφ+24∫π6π3cosφ·sinφdφ==12∫π6π3(1+cos2φ)dφ+24∫π6π3sinφd(sinφ)==12·φ+12sin(2φ)π6π3+12·sin2φπ6π3==12·π3+12sin2π3-π6+12sin2π6+12·sin2π3-sin2π6==12·π6+12·322-122=2π+6

Ответ: S(G)=2π+6

Вычисление площадей фигур, изображенных на клетчатой бумаге



При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?

Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.

Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.

Возможны следующие случаи.

1. Фигура представляет собой треугольник, параллелограмм, трапецию:

1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;

2) подставить найденные величины в формулу площади.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.

Рис. 1. Треугольник

Решение. Подсчитываем клеточки и находим: . По формуле получаем: .

2 Фигура представляет собой многоугольник

Если фигура представляет собой многоугольник то возможно использовать следующие методы.

Метод разбиения:

1) разбить многоугольник на треугольники, прямоугольники;

2) вычислить площади полученных фигур;

3) найти сумму всех площадей полученных фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.

Рис. 2. Многоугольник

Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.

Рис. 3. Многоугольник. Метод разбиения

Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:

Метод дополнительного построения

1) достроить фигуру до прямоугольника

2) найти площади полученных дополнительных фигур и площадь самого прямоугольника

3) из площади прямоугольника вычесть площади всех «лишних» фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.

Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.

Рис. 4. Многоугольник. Метод дополнения

Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .

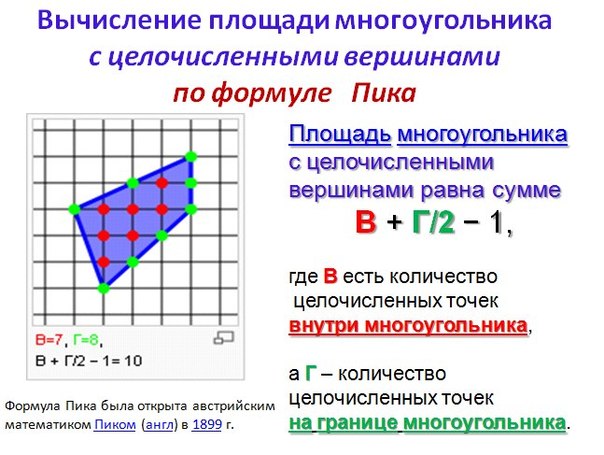
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.

Формула Пика

Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.

Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

Например, для многоугольника, изображенного на рисунке 5.

Рис. 5. Узлы в формуле Пика

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.

Рис. 6. Многоугольник. Формула Пика

Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:

Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.

1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.

Рис. 7. Условие задачи 1

2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).

Рис. 8. Условие задачи 2

3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.

Рис. 9. Условие задачи 3

4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.

Рис. 10. Условие задачи 4

5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.

Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.

Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.

Литература:

1. Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
2. Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
3. Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.

Основные термины (генерируются автоматически): формула Пика, клетчатая бумага, площадь фигуры, фигура, вычисление площадей, многоугольник, площадь, размер клетки, условие задачи, универсальная формула.

Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора

Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = w × h
w = ширина
h = высота

Мы знаем, что w = 5 и h = 3 , поэтому:

Площадь = 5 × 3 = 15

Пример: Какова площадь этого круга?

Радиус = r = 3

Площадь		= π × r 2
		= π × 3 2
		= π × (3 × 3)
		= 3.14159 … × 9
		= 28,27 (до 2 знаков после запятой)

Пример: Какова площадь этого треугольника?

Высота = h = 12

База = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Более сложный пример:

Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр

Сколько зарабатывает Сэм, обрабатывая эту область:

Разобьем область на две части:

Часть A — квадрат:

Площадь A = a ² = 20 м × 20 м = 400 м ²

Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итого общая площадь:

Площадь = Площадь A + Площадь B = 400 м ² + 140 м ² = 540 м ²

Сэм зарабатывает 0,10 доллара за квадратный метр

Сэм зарабатывает = 0,10 доллара × 540 млн ² = 54 доллара

Калькулятор площади

— Расчет площади различной формы

Вычислите площадь, выбрав форму и введя свои измерения в любых метрических или обычных единицах США.См. Формулы для расчета площади каждой формы ниже.

Как рассчитать площадь

Площадь — это пространство внутри периметра / границы пространства, его символ — (A). Это размер двухмерной поверхности и измеряется в квадратных единицах, например квадратных футах.

Квадратные футы также могут быть выражены в футах ² или в квадратных футах. Используйте наши формулы, чтобы найти площадь многих форм.

Перед вычислением площади важно измерить все длины в одной и той же единице измерения или преобразовать все длины в одну и ту же единицу.Воспользуйтесь нашими калькуляторами преобразования единиц длины или калькуляторами преобразования единиц площади для преобразования британских единиц измерения в метрические.

Используйте приведенные ниже формулы, чтобы рассчитать площадь многих популярных фигур.

---

Формула площади

А = а ²
А = а × а

a = длина кромки

---

Формула площади прямоугольника

A = длина × ширина

l = длина
w = ширина

---

Формула приграничной площади

А = (l1 × w1) — (l2 × l2)

l1 = внешняя длина
w1 = внешняя ширина
l2 = внутренняя длина
w2 = внутренняя ширина

---

Формула площади трапеции

A = ¹ / ₂ (a + b) h

a = основание a
b = основание b
h = высота

---

Формула площади параллелограмма

A = b × h

b = основание
h = высота

---

Формула площади треугольника

s = ¹ / ₂ (a + b + c)
A = s (s — a) (s — b) (s — c))

a = край a
b = край b
c = край c

Эта формула известна как формула Герона. Вы также можете использовать упрощенную формулу, если известна высота треугольника.

A = ¹ / ₂ bh

b = край b
h = высота

---

Формула площади круга

А = πr ²

r = радиус

Если вам известен диаметр окружности, вы можете найти радиус, разделив диаметр пополам.

Знаете ли вы, что у нас также есть калькулятор для определения площади круга?

---

Формула площади эллипса

А = πab

a = ось a
b = ось b

---

Формула площади сектора

А = (θ ÷ 360) πr ²

r = радиус
θ = угол

Узнайте больше о секторах и посмотрите более подробные примеры в нашем калькуляторе площади секторов.

---

Формула площади правильного многоугольника

A = (a ² × n) ÷ (4 × tan (π ÷ n))

a = длина кромки
n = количество сторон

---

Неправильные многоугольники и сложные формы

Уловка для определения площади неправильного многоугольника или сложной формы состоит в том, чтобы сначала разбить форму на правильные многоугольники, такие как треугольники и квадраты, затем найти площадь этих фигур и сложить их вместе, чтобы найти общую сумму.

---

Разница между площадью и площадью

Вам может быть интересно, чем площадь отличается от площади поверхности.В то время как площадь — это размер двухмерной плоскости, площадь поверхности — это размер поверхности трехмерной твердой формы.

Разница между площадью и периметром

Так в чем же разница между периметром и площадью? Периметр — это расстояние вокруг двухмерной фигуры, а площадь — это размер самой фигуры.

Конечно, у нас есть калькулятор периметра, который поможет решить эту проблему с измерением длины.

Калькулятор свободной площади

Введите два значения.Остальные значения будут рассчитаны. Сторона а: Сторона b: площадь Периметр: диагональ

Этот калькулятор вычисляет значения круга (радиус, диаметр, окружность или площадь), когда задано одно значение. Заполните одно поле. Остальные будут рассчитаны. Радиус r: Диаметр d: Периметр U: Площадь A:

Этот калькулятор вычисляет из трех значений треугольника все остальные значения. Введите три значения. Остальные значения будут рассчитаны. а: б: c: альфа: бета: гамма: Высота: h a : Высота: h b : Высота: h c : Площадь Не часто требуется (пустите, если не нужно): Средняя линия: с a : s b : с с : Биссектриса угла: w a : w b : w c :

Вычислить квадрат Введите одно значение. Остальные значения будут рассчитаны. Сторона Площадь: Периметр: диагональ

Введите два значения. Остальные значения будут рассчитаны. Сторона А: Диагональ e: Диагональ f: альфа бета Периметр: Площадь:

Введите здесь одну функцию.2 для.

Если у вас есть некоторая информация о вашем районе, вопрос в том, как рассчитать другие данные. Во многих случаях это возможно. Квадрат или круг, например уже даны одной информацией (например, периметр или площадь). Наличие областей с меньшей симметрией означает, что нам нужно больше информации. В Mathepower есть много вычислителей площади.

Калькуляторы по этой теме:
Калькулятор треугольников
Калькулятор круга
Калькулятор дуги
Калькулятор ромбовидной формы
Калькулятор квадратов
Калькулятор ромбов
Калькулятор прямоугольников
Калькулятор трапеций

Расчет площади

Для правильного выполнения рекомендаций по удобрениям при испытании почвы необходимы две основные части информации.

1. Насколько велика площадь удобрения?

2. Сколько удобрений необходимо внести, чтобы обеспечить это количество рекомендованных питательных веществ?

Насколько велика площадь для удобрения?

Первый шаг при внесении удобрений — определить, сколько квадратных футов земли нужно удобрить. Это требует некоторой геометрии. Поначалу это может показаться трудоемким.Однако вам нужно сделать это только один раз, если вы храните информацию в файле.

Большинство следующих примеров относятся к простым формам. Выберите форму или комбинацию форм, которые наиболее точно соответствуют площади, которую нужно удобрять, чтобы рассчитать площадь земли. Многие участки земли, подлежащие удобрению, имеют очень неправильную форму. В этом случае вы можете использовать метод смещения, описанный в последнем примере.

Формы и формулы

Эти формы определяются прямыми, параллельными противоположными сторонами и одинаковой длиной.Площадь всех трех форм определяется умножением длины (L) на ширину (W).

Формула
Площадь = L (длина) x W (ширина)
Пример
Площадь = L (длина) x W (ширина) L = 75 футов, W = 25 футов • Площадь = 75 x 25 • = 1875 футов 2

Круг

Площадь круга находится путем умножения константы пи (p или 3. 14) умноженный на квадрат радиуса. Радиус равен диаметру.

Формула
Площадь = π x r 2 • π (пи) = 3,14 • r 2 (квадрат радиуса) = r x r
Пример
Площадь = π x r 2 • r = 6 футов Площадь = π x r 2 • = 3,14 x (6 x 6) • = 3.14 х 36 • = 113 футов 2

Треугольник

Площадь треугольника определяется путем умножения длины основания на длину высоты и последующего деления полученного результата на 2.

Формула
Площадь = (ш x в) 2 • b = длина основания • h = длина высоты
Пример
Площадь = (ш x в) 2 • b = 10 футов, h = 5 футов Площадь = (ш x в) 2 • = (10 x 5) 2 • = 50 2 • = 25 футов 2

Трапеция

Площадь трапеции определяется сначала путем нахождения средней длины параллельных сторон (A + B) 2, а затем умножения результата на высоту (h).

Формула
Площадь = [(A + B) 2] x h
Пример
Площадь = [(A + B) 2] x h • A = 20 футов, B + 10 футов, h = 5 футов Площадь = [{A + B) 2] x h • = [(20 + 10) 2] x 5 • = [30 2] x 5 • = 15 x 5 • = 75 футов 2

Овальный

Площадь овала находится путем умножения ширины (W) на длину (L) и последующего умножения результата на 0.8

Формула
Площадь = (Ш x Д) x 0,8 • W = ширина • L = длина
Пример
Площадь = (Ш x Д) x 0,8 • W = 10 футов, L = 20 футов Площадь = (Ш x Д) x 0,8 • = (10 x 20) x 0,8 • = 200 x 0,8 • = 160 футов 2

Внесение удобрений в области вокруг объекта или дерева

Если вы хотите внести удобрения в области вокруг объекта, например беседки, отдельного ландшафтного участка или хвойного дерева, конечности которого касаются почвы, вам необходимо внести два расчета. Определите площадь внутренней, неоплодотворенной области, используя соответствующую формулу, а затем определите размер большей области, которая охватывает внутренний объект. Затем вычтите внутреннюю область из внешней. Результатом будет площадь в квадратных футах удобряемой площади (в данном примере — «форма пончика»).

Формула
Площадь удобрения = Площадь внешнего круга (π R 2 ) — Площадь внутреннего круга (π r 2 )
Пример
Площадь удобрения = Площадь внешнего круга (π R 2 ) — Площадь внутреннего круга (π r 2 ) • R = 6 футов, r = 3 фута Площадь удобрения = Площадь внешнего круга (π R 2 ) — Площадь внутреннего круга (π r 2 ) • = [3.14 x (6 x 6)] — [3,14 x (3 x 3)] • = [3,14 x 36] — [3,14 x 9] • = 113–28 • = 85 футов 2

Составные простые формы

Многие области ландшафта можно разделить на несколько простых форм. В этих случаях используйте формулы для простых форм и сложите результаты для общей площади в квадратных футах. См. Соответствующую формулу в других разделах этой статьи.

Нечетные формы

Метод, используемый для областей неправильной формы, называется «методом смещения».Сначала измерьте длину самой длинной оси участка (линия AB). Это называется линией длины . Затем разделите линию длины на равные части, например, 10 футов. В каждой из этих точек измерьте расстояние по площади на линии, перпендикулярной линии длины в каждой точке (линии от C до G). Эти линии называются линиями смещения . Наконец, сложите длины всех линий смещения и умножьте результат на расстояние, разделяющее эти линии (10 футов в этом примере).

Пример

Длина линии (AB) = 60 футов, расстояние между линиями смещения составляет 10 футов друг от друга • Длина каждой линии смещения C = 15 футов, D = 10 футов, E = 15 футов, F = 25 футов, G = 20 футов Общая длина линий смещения = C + D + E + F + G • = 15 + 10 + 15 + 25 + 20 • = 85 футов Площадь для удобрения = Расстояние между линиями смещения x сумма длины линий смещения • = 10 футов x 85 футов • = 850 футов 2

Прочие формулы

Форма	Формула
Пентагон (5 равных сторон)	(длина 1 стороны) 2 x 1. 7
Шестигранник (6 равных сторон)	(длина 1 стороны) 2 x 2,6
Восьмиугольник (8 равных сторон)	(длина 1 стороны) 2 x 4,84

Расчетная область — archtoolbox.com

Ниже представлена ​​серия диаграмм, демонстрирующих, как рассчитать площадь двумерных фигур.

Площадь круга

Площадь круга равна произведению числа Пи на квадрат радиуса.

Площадь = pi (r x r)

Площадь круга

---

Площадь эллипса

Эллипс представляет собой плоский круг, поэтому при вычислении площади учитывается наличие двух разных радиусов.

Площадь = pi (r1 x r2)

Площадь эллипса

---

Площадь треугольника

Площадь треугольника равна половине произведения основания и высоты.

Площадь = (h x B) / 2

Площадь треугольника

---

Площадь равностороннего треугольника

Равносторонний треугольник имеет 3 стороны равной длины. Хотя приведенная выше формула также будет работать, существует альтернативный метод вычисления площади равностороннего треугольника.

Площадь = ((sqrt 3) (A x A)) / 4

Площадь равностороннего треугольника

---

Площадь прямоугольника

Площадь прямоугольника равна произведению длинной стороны и короткой стороны.Площадь квадрата — это длина стороны в квадрате.

Площадь = A x B

Площадь прямоугольника

---

Площадь параллелограмма

Параллелограмм — это слегка скошенный прямоугольник. Площадь — это произведение основания и общей высоты.

Площадь = B x h

Площадь параллелограмма

---

Площадь трапеции

Трапеции — половина параллелограмма. На диаграмме слева показано, как две равные трапеции образуют параллелограмм.Следовательно, расчет площади — это просто половина площади параллелограмма.

Площадь = 1/2 (h (A + B))

Площадь трапеции

---

Площадь четырехугольника

Четырехугольник — это просто два сложенных вместе треугольника, поэтому площадь можно вычислить, сложив площади двух треугольников.

Площадь — (1/2 (h ₁ x B)) + (1/2 (h ₂ x B))

Площадь четырехугольника

Статья обновлена: 8 сентября 2019 г.

Connect IQ Store | Бесплатные циферблаты и приложения

이재윤
29 января 2021 г. | Версия 2.7,5

사용 하기 좋아요

Тео Кэмпбелл
11 ноября 2020 г. | Версия 2.7.5

Я знаю, что это не связано в частности с этим программным обеспечением (на самом деле это отчет об ошибке для приложения ConnectIQ (и, возможно, прошивки предшественника 245)), но есть странная ошибка, из-за которой некоторые приложения обновляются несколько раз для одного и того же обновления. Другое дело, что индикатор доступного места на часах никогда не обновляется (для меня он застрял на 15/31). Последнее, что происходит, это то, что в приложении возникает тупик после первой упомянутой ошибки, и ничто не может обновить или установить пока я не перезапущу приложение.Актуальный обзор ниже. Единственная причина, по которой я удалю это, состоит в том, что я действительно не буду им пользоваться. Тем не менее, я поставлю этому обзору 5 звезд, потому что предполагаю, что это хорошее приложение, которое даст точные результаты.

Педро
27 сентября 2020 г. | Версия 2.7.3

Falta poder descargar y ver despues el calculo de área realizado ..

Харви Гомес Сабогал
19 сентября 2020 г. | Версия 2.7,3

Sería bueno q se pudiera descargar el el mapa y la medición realizada

Якуб Зитко
12 мая 2020 г. | Версия 2.7.2

Здравствуйте, меня зовут Джейкоб, и у меня есть проблемное приложение, которое я установил, но у меня его нет в моих часах, мои часы называются garmin viviactive 3, не могли бы вы мне помочь. и извиняюсь за ошибки, я из Чехии. Спасибо Джейкобу.

Рудреш Оджа
21 сентября 2019 г. | Версия 2.7,1

Установлен на предшественник 245 M, но не может подключиться к GPS. В чем может быть проблема. Спасибо +919415304802

kpgcfd
18 сентября 2019 г. | Версия 2.7.1

Я ждал, что это сработает с моим vivoative 3, наконец-то оно работает !!. Это одна из основных причин, по которой я купил vivoative 3 после того, как у меня был vivoactive hr, и он умер.

Гильермо Арсе
9 ноября 2018 г. | Версия 2.6-upd6

Отлично, но можно ли использовать с GPS или GPS + ГЛОНАСС?

😎Ty🏆Waldnr😎
24 октября 2018 г. | Версия 2.6-upd6

Даст 5 звезд, как только вы сделаете совместимым с Vivoactive 3

ЖЕЛЕЗНЫЙ ЧЕЛОВЕК
21 марта 2018 г. | Версия 2.6-upd5

Очень очень хорошо!!!

Νικος
9 февраля 2018 г. | Версия 2.6-upd3

Отлично!!! Просто отлично !!!

phlame64
12 сентября 2017 г. | Версия 2.6-upd

Отлично работает на моем Fenix ​​5X!

clodeczm
12 мая 2017 г. | Версия 2.5

Когда он будет совместим с Fenix ​​5x?

Т. Зимми
5 января 2016 г. | Версия 2.3

Отлично работает для vivoactive.Но было бы интереснее рассчитать площадь, сохранив несколько точек GPS, потому что иногда между точками есть препятствия.

Сергей К.
28 декабря 2015 г. | Версия 2.3

Это очень интересно, а как сбросить расчет на 0? У вас есть тема на форуме Garmin для этого приложения?

Д’мо Иосифидис
25 декабря 2015 г. | Версия 2.3

Это делает работу

Enigma Delta
25 ноября 2015 г. | Версия 2.3

Отличное приложение, я использую его для проверки областей, которые я измерил для работы. Надеюсь, что Garmin добавит функцию Distance / Lenght для измерения расстояния.

Luc
24 ноября 2015 г. | Версия 2.3

Fonctionne très bien sur ma Vivoactive. J’aurais toutefois souhaité que les вычисления du perimètre apparaissent в Garmin Connect для будущих консультаций.

ВАСИЛИЙ МАГИАР
8 сентября 2015 г. | Версия 2.2

после завершения измерения, где находится файл?

neo.juampa
15 июля 2015 г. | Версия 2.1

Приложение Muy buena! Un accesorio muy útil para un gps de muñeca. Sí, sería muy buena idea que se pueda guardar con nombre, fecha y posición geográfica tanto el perímetro como el área calcada.

Юлиус Кан
19 мая 2015 г. | Версия 2.0

Отличное приложение. Прекрасно работает.

PLPF3
27 апреля 2015 г. | Версия 2.0

Para hacerla mas útil estaría muy bien poder guardar el track del perímetro recorrido.

Как рассчитать квадратные футы неправильных форм

Как определить квадратные ножки неправильной формы

Поскольку ваша евклидова геометрия может быть немного ржавой, у нас есть несколько формул, которые помогут вам определить, сколько квадратных футов стекла у вас есть в вашем проекте.Чтобы перевести американские единицы измерения в метрические единицы, нажмите здесь

Большое спасибо Алексу Стассеру за разрешение показать его «Soft Bar Bells».

Постоянные числа

Постоянные числа — это числа, одинаковые для всех формул. Постоянные числа для наших формул:

• π = 3,142. π (пи) — это отношение диаметра к длине окружности.
  Лучше всего выражается как 22/7. Вычислить проще, если вы используете (приблизительное) число 3.142
• 144 = 12 дюймов x 12 дюймов = количество квадратных дюймов в 1 квадратном футе.
  Вычислить проще, если вы измерите все в дюймах и разделите окончательный ответ на 144, чтобы найти количество квадратных футов.

Радиус

• r = радиус. Радиус круга равен 1/2 диаметра. Пример, круг диаметром 36 дюймов имеет радиус 18 дюймов.
• r ² = радиус, умноженный на радиус, а не радиус, умноженный на 2. Пример 18 дюймов x 18 дюймов = 324 дюйма; не 36 дюймов

Чтобы найти радиус сферы :

1. Измерьте расстояние вокруг сферы, чтобы найти длину окружности.
2. Разделите длину окружности на 3,142 (π), чтобы найти диаметр.
3. Разделите диаметр на 2, чтобы найти радиус.

Формулы для плоского стекла

• Прямоугольник или квадрат = длина x ширина
• Круг = π x r ²
• Овал или эллипс = π x большая ось x малая ось. Большая ось составляет 1/2 длины. Малая ось составляет 1/2 ширины.

Пример 1 — Круг диаметром 15 дюймов:

1. 15 ÷ 2 = 7,5 (радиус)
2. 7,5 x 7,5 = 56,25 (радиус в квадрате)
3. 56,25 x 3,142 = 176,79 (квадрат радиуса, умноженный на пи)
4. 176,79 ÷ 144 = 1,23 квадратных футов (квадратные дюймы, преобразованные в квадратные футы)

Пример 2 — Овал длиной 18 дюймов и шириной 10 дюймов

1. 18 ÷ 2 = 9 (большая ось)
2. 10 ÷ 2 = 5 (малая ось)
3. 3. 142 x 9 x 5 = 141 (π x большая ось x малая ось)
4. 141 ÷ 144 = 0,98 (квадратные дюймы преобразованы в квадратные футы)

Формулы для выдувного стекла

Помните, что вам нужно знать площадь поверхности, , а не объем . Длинная тонкая трубка имеет меньшую площадь поверхности, чем глобус того же объема.
Как ты делаешь математику? Самый простой способ — мысленно разделить предмет на участки правильной формы.Например, объект в форме карандаша можно представить себе как цилиндр с конусом на вершине.

Формулы для выдувного стекла

• Сфера = 4π r ² .
• Открытый цилиндр = 2π r l где «r» — радиус поперечного сечения, «l» — его длина
• Открытый конус = π x r x s , где «r» — радиус поперечного сечения основания, «s» — длина стороны
• Прямоугольная коробка = w x h x l , где «w» — ширина, «h» — высота, «l» — длина

Пример 1 — Вы зеркалируете внутреннюю часть стеклянной чаши диаметром 34 дюйма. Представьте себе чашу в виде полусферы. Радиус чаши составляет половину диаметра или 17 дюймов. Используя приведенную выше формулу, площадь поверхности полусферы равна 1/2 от 4πr ²

• 1/2 из 4πr ² = 2πr ²
• 2 x 3,142 x17 x 17 = 1816,65 квадратных дюймов
• 1816,65 ÷ 144 = 12,62 квадратных футов

Пример 2 — У вас есть колокольчик из дутого стекла — другими словами, с парой лампочек, соединенных трубкой.Конечно, вам понадобится отверстие, куда вы сможете заливать и сливать жидкости.

• Допустим, колбы имеют диаметр 3 дюйма, поэтому их радиус составляет 1,5 дюйма. Поскольку лампы в основном представляют собой сферы, используется формула 4πr ²
  4 x 3,142 x 1,5 x 1,5 ÷ 144 = 0,2 квадратных фута

• Предположим, что соединяющая их труба имеет длину 1 фут и диаметр 1,5 дюйма. Радиус будет 0,75 дюйма. Трубка представляет собой открытый цилиндр и используется формула 2πrl.
  2 x 3,142 x 0,75 x 12 ÷ 144 = 0,4 квадратных фута

• Таким образом, общая площадь поверхности двух сфер плюс цилиндр составляет
  0,2 + 0,2 + 0,4 = 0,8 квадратных футов

Это позволяет использовать ту часть сферы, которая отсутствует из-за присоединения к трубке.

Формулы для трехмерного стекла

При зеркальном отображении 3-D стекла используйте формулу, которая соответствовала бы вашей форме, если бы стекло не имело неровной поверхности. На небольшие кусочки используйте всего 15 мл (по 5 мл каждой жидкости), чтобы получить достаточное покрытие.

.