Узнать площадь: Онлайн калькулятор. Площадь прямоугольника

Нахождение площади квадрата

В геометрии квадратом называется четырехугольник, у которого все углы составляют 90°, а все стороны равны. С тем, как вычислить площадь квадрата, все мы сталкивались еще на школьных уроках, так что эта процедура ни у кого не вызывает никаких трудностей. На практике заниматься такого рода расчетами довольно часто приходится специалистам в области строительства, продажи и обмена недвижимости.

Нахождение площади квадрата

Формула расчёта площади квадрата

 

S = а2

 

а – сторона квадрата

S – площадь квадрата

 

Ее площадь в России и других странах, придерживающихся метрической системы мер, определяется в квадратных метрах, то есть в количестве квадратов, длина стороны которых составляет один метр. Поскольку то, как посчитать площадь квадрата, знают все, то и определить размер общей или жилой площади не составляет труда, что критически важно при определении стоимости того или иного объекта недвижимости.

Специалистам, производящим внутреннюю отделку помещений, также необходимо знать то, как вычислить площадь квадрата. В данном случае также имеется в виду квадратный метр, поскольку расценки на работы у них определяются именно исходя из этой величины. Кроме того, им требуется вычислить необходимое количество материала, расход которого, к примеру, в случае с краской и лаками измеряется такой величиной, как граммы на квадратный метр. Что касается керамической плитки, имеющей квадратную форму, то тем мастерам, которые занимаются ее укладкой на стены и пол, также нужно знать ее площадь, чтобы определить требуемое количество кафеля.

Всем автомобилистам знакомы дорожные знаки, имеющие квадратную форму. Само собой разумеется, что тем специалисты, которые в свое время занимались их разработкой и созданием на них технической документации, не смогли бы справиться со своей задачей, если бы не знали,

как вычислить площадь квадрата.

В современной картографии широко используется разбиение на квадраты для того, чтобы имелась возможность точно определять как площадь той или иной местности, так и соответствующие параметры любой ее точки. Для этого используется двумерная система, в которой положение того или иного ее объекта характеризуется его координатами по осям X и Y, выраженным в некотором абсолютном значении относительно исходной точки O.

Наконец, такая геометрическая фигура, как квадрат, «отметилась» и в столь далекой от точных наук сфере, как абстракционизм. Произошло это благодаря небезызвестному художнику Казимиру Малевичу, который в свое время написал свой шедевр «Черный квадрат», впоследствии вошедший в сокровищницу мировой культуры как по значимости для мировой культуры, так и по рекордно высокой оценочной стоимости этого выдающегося полотна.

Площадь фигуры / Основы геометрии / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Основы геометрии
5. Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Например, площадь в городе  — это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.

---

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

---

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

---

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник : 

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

---

Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками. 

Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

---

Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади –

квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

1 дм² = ? см²

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

10  • 10 = 100 см²

Значит, 1 дм² = 100 см²

---

Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

---

---

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

---

Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

---

Ар

Ар — это площадь квадрата со стороной 10 м.

Слово «ар» при числах сокращённо записывают так:

1 а, 20 а, 97 а.

1 а² = 100 м², поэтому ар часто называют соткой.

---

Гектар

Гектар — это площадь квадрата со стороной 100 м.

Слово «гектар» при числах сокращённо записывают так:

1 га, 20 га, 530 га.

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

---

Ар и гектар используются при измерении земельных участков.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Площадь прямоугольника

Круг. Шар. Овал

Треугольники

Многоугольники

Угол. Виды углов

Обозначение геометрических фигур буквами

Периметр многоугольника

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

2 класс

Страница 41. Урок 16, Петерсон, Учебник, часть 2

Страница 43. Урок 17, Петерсон, Учебник, часть 2

Страница 45. Урок 17, Петерсон, Учебник, часть 2

Страница 50. Урок 19, Петерсон, Учебник, часть 2

Страница 58. Урок 23, Петерсон, Учебник, часть 2

Страница 61. Урок 24, Петерсон, Учебник, часть 2

Страница 68. Урок 27, Петерсон, Учебник, часть 2

Страница 79. Урок 32, Петерсон, Учебник, часть 2

Страница 82. Урок 34, Петерсон, Учебник, часть 2

Страница 91. Урок 38, Петерсон, Учебник, часть 2

3 класс

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 109, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 41, Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 55, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1

Страница 51, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 76, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 28. Вариант 1. Проверочная работа 3, Моро, Волкова, Проверочные работы

Страница 33. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

Страница 14, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 43, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 65, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 72, Моро, Волкова, Рабочая тетрадь, часть 2

---

© budu5. com, 2021

Пользовательское соглашение

Copyright

Площадь круга | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Для того чтобы найти площадь круга, существует единственная формула, которую нужно запомнить – это произведение числа π на квадрат радиуса.
Доказательством этой формулы будет служить следующий расчет. На чертеже внутри и снаружи круга рисуем правильный многоугольник – многоугольник с равными сторонами.

Из центра круга проводим радиусы в указанные вершины многоугольников. Радиусы во вписанном многоугольнике делят его на определенное количество n одинаковых равнобедренных треугольников. Таким образом, площадь вписанного многоугольника – это n площадей треугольников S_в=nS_∆. Тогда как площадь каждого треугольника, исходя из его свойств, равна . Так как конгруэнтные стороны a этого треугольника являются радиусами, то формула приобретает вид , а формула площади всего многоугольника – , считая сумму всех сторон nc, как периметр многоугольника P. Аналогично получаем площадь описанного многоугольника: . Если считать, что количество nc, как сторон многоугольника стремится к бесконечности, то его форма максимально приближается к кругу, и периметр становится близок по значению к длине окружности, а cosα стремится к 1. В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:

---

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности.
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два. Так как в первоначальной формуле S=πr² радиус возводится во вторую степень, полученная половина диаметра также должна будет быть в квадрате, и это уже будет выглядеть как .

---

Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель: . Подставляя это в основную формулу, не забываем возвести выражение во вторую степень, и получаем, что площадь круга через длину окружности равна .

Как посчитать площадь листа. Как узнать площадь комнаты? Измерение площади прямоугольных помещений

Площадь помещения определяется после отделки стен и перегородок как площадь на уровне пола без учета плинтусов

Любое важное начинание надо просчитывать заранее, ремонт не исключение. Поскольку затраты предстоят большие, надо их оптимизировать и уменьшить по максимуму, особенно, если хочется сделать что-то дорогостоящее, например натяжные потолки с несколькими уровнями. Если покупать материалы «на глазок», легко можно ошибиться – купить или слишком много или придется идти в магазин и докупать недостающие стройматериалы. Для того, чтобы не купить лишнего дорогого стройматериала и сэкономить семейный бюджет, надо знать, как рассчитать площадь помещения.

Жилой принято считать отдельную комнату, с наличием условий для проживания людей. Пригодные для жилья комнаты должны соответствовать всем требованиям, изложенным в действующих строительных нормативных документах. Метраж жилой площади общественного дома и каждого его этажа вычисляется путем сложения метража квартир.

При вычислении метража жилого помещения, слагают метраж всех его комнат, включая имеющиеся подсобные помещения. Подсобными принято считать следующие объекты:

Жилое помещение – изолированное помещение, которое является недвижимым имуществом, пригодное для постоянного проживания людей

В сооружениях, включающих один этаж, метраж лоджий, балконов, террас, а также веранд в площадь жилого помещения не учитывается. В многоэтажных домах в эту категорию входят подполья для проветривания, построенного на постоянно мерзлом грунте, нежилое чердачное помещение, внеквартирные коммуникации, лестничные конструкции, расположенные вне помещения.

Особенности расчета площади помещений

Чтобы вычислить общий метраж квартиры, нужно найти сумму площадей ее жилых и подсобных комнат. Для выполнения точного расчета обязательна корректировка вычислений. При этом следует использовать специальные понижающие коэффициенты. Для определения метража лоджий коэффициент составляет 0.5, для террас и балконов – 0.3, для холодных кладовых и веранд корректировка равна 1.0.

Чтобы вычислить общий метраж многоэтажного дома находят сумму площадей подземного этажа (технического) и наземных (включая мансардный этаж). К общему метражу также относятся незакрытые неотапливаемые объекты сооружения.

Общий метраж этажа можно посчитать путем измерения его параметров между внутренними поверхностями стен, ограждений и перегородок с финишной отделкой. В общий метраж каждого уровня многоэтажного здания включают размер пространства между маршами лестниц, а также проемы в горизонтальных перекрытиях размером более 36 м.кв. При вычислении общего метража помещения не учитывают размеры этажа технического назначения, высотой до 1.8 м.

Общая площадь квартиры – метраж, включающий в себя все помещения квартиры, вне зависимости от того, жилые они или вспомогательные

Последовательность выполнения расчетов площади помещений

Проще всего узнать площадь жилого помещения в виде прямоугольной или квадратной фигуры. Для этого необходимо найти значения его длины и ширины, а затем их перемножить. Рекомендованные единицы измерения параметров помещений – метры, а площадь выражается в метрах квадратных. Все необходимые измерения проводят рулеткой по полу между поверхностями стен, не учитывая плинтусы.

Отдельно находят метраж имеющихся выступающих конструктивных частей помещения, ниш и углублений. Размеры объектов, которые выступают в зону помещения, вычитают из общего метража, а величину ниш и углублений прибавляют.

Важно!

Пространство помещения, занимаемое отопительными элементами, при вычислении общего жилого метража сооружения во внимание не принимается.

Если размер помещений нужен для того, чтобы узнать необходимое количество стройматериалов, из площади стен исключают размеры дверных, оконных проемов и прибавляют площадь углублений под радиаторы отопления.

Если помещение имеет сложную форму, для упрощения подсчетов его разбивают на квадраты и прямоугольники, треугольники или сектора круга. Чтобы вычислить общий размер, суммируют найденные параметры всех участков помещения.

Измерение площади и объема помещения лазерным дальномером

S = v*(р*(р-а)*(р-b)*(р-с)) , где величина S является полупериметром треугольника, a , b , c – значения длины его сторон.

P = (а+b+с)/2

Для осуществления расчетов площади равностороннего треугольника можно использовать следующую формулу:

S = S² , где S – значение длины его стороны.

Размер площади прямоугольного треугольника представляет собой произведение длин сторон, составляющих прямой угол, поделенное на 2. Для расчетов также можно использовать значения высоты и основания треугольника. В этом случае, площадь его находится по формуле:

S =1/2*h*b , где h – значение высоты треугольника, b – величина его основания.

С помощью всего лишь двух или трех измерений вы сможете быстро и точно рассчитать площадь потолка, пола или стены, а также объем помещения

Также существует способ расчета, если известны размеры двух сторон треугольника и образованного между ними угла: S =1/2*c*b*sinA , где с и b – длина сторон, A – угол между ними. Согласно формуле, произведение длин сторон делят пополам, а затем результат умножают на значение синуса известного угла. Синус угла возможно найти по таблице Брадиса либо определить на калькуляторе.

Для выполнения вычислений площади круга можно пользоваться всем известной формулой S = πr2 , где π=3.14 , r – значение радиуса круга (половина диаметра). Следовательно, метраж полукруга находят, разделив площадь круга на 2.

Как найти метраж мансардного этажа

Мансардный этаж относится к помещениям, пригодным для проживания людей. Чтобы определить его площадь, не достаточно умножить значение высоты на ширину и длину прямоугольного пола. Если мансардный этаж выполнен в сложной форме, его пространство делят на участки и суммируют их метраж.

Поэтому, чтобы найти максимально точное значение площади мансарды, считают размер высоты наиболее узкой части ската крыши – 1.5 м, если уклон равен 30° , 1.1 м – если угол уклона 45° , 0.5 м – угол 60° . Если чердачный этаж ниже полуметра, необходимо умножать общий метраж на коэффициент со значением 0.7.

Важно!

При расчете параметров жилого пространства мансардного этажа необходимо считать величину от пола до изгиба скатов. Если данная величина составляет менее 90 см, она является глухой и не учитывается в полезную площадь.

Если уклон скатов крыши составляет 45 градусов, метраж можно посчитать по формуле, которая будет выглядеть как: S = A*L + 2В*0.7*L= L*(A+1.4B) . Где S – метраж пола мансарды, L – длина, А и В – значения ширины пола при высоте 1.1 и 0.8 метров. 0.7 – размер поправки, по которой осуществляется корректировка расчета метража мансарды.

Корректировка на площадь при оценке помещения

Для того чтобы самостоятельно определить стоимость здания в зависимости от его площади, следует считать определенные поправки. Зачастую, с увеличением метража оцениваемого здания, стоимость м. кв. снижается. Исходя из этого, корректировка на площадь заключается в снижении стоимости 1 м.кв. на 1 % с увеличением метража на каждые 5 м.кв.

Также, на стоимость недвижимости оказывает влияние размер кухни. Поэтому применяется корректировка из расчета 0.5 % на разницу в 1 м.кв.кухни.

Учитывая рекомендации, как следует считать площадь помещений и зданий, можно самостоятельно определить размеры недвижимости и сравнить их с данными технической документации. Используя полученные результаты можно определить потребности в отделочных стройматериалах или выяснить стоимость жилья.

Как делать обмеры интерьера – замеры интерьера

Ремонт пола в квартире или доме требует точного расчета количества м2 в каждой комнате. В связи с тем, что на сегодняшний день строительные материалы — товар достаточно дорогой, каждый, кто затеял ремонт, пытается как можно больше сэкономить на материалах. Если вы не знаете, как правильно посчитать площадь неровного пола, который имеет нестандартные размеры — эта статья расскажет вам об этом.

Для чего могут пригодится расчеты?

Для чего нужно рассчитывать площадь пола:

• Чтобы купить необходимое количество материалов;
• Сэкономить на покупке напольного покрытия;
• Для того, чтобы определить количество жилой помощи в помещении;
• После строительства дома для определения соответствия с планом;
• При ремонте, для определения размеров будущей мебели и т. д;

Причин, по которым нужно вычислить площадь помещения — множество, решений же существует несколько.

Вычисление площади пола

Если комната стандартная (квадратная или прямоугольная), то вычислить площадь такого помещения сможет каждый. Для этого нужно узнать ширину и длину помещения, после чего просто перемножить эти показатели.

Таким образом, формула будет выглядеть так: S = a * b, где, а и b — длина и ширина помещения.

Если вы рассчитываете площадь помещения для потолка, то встроенные шкафы или камины никак не повлияют на замеры площади.

В случае, если вы собираетесь установить камин или же установить встроенный шкаф-купе, то площадь, которую он будет занимать, нужно обязательно вычислить исходя из предполагаемых размеров конструкции и общих размеров помещения.

Проводить точные замеры помещений, в которых имеется встроенная мебель, необходимо, если вы планируете укладывать напольное покрытие. В случае, если камин или комод занимает не много места, его площадью можно пренебречь, если много — конструкцию на время можно разобрать или высчитать сколько места она занимает.

Как высчитать площадь пола с неправильными размерами?

Если комната имеет нестандартные размеры — вычисление площади пола будет происходить немного дольше и сложнее. Существует множество причин, по которым комната может иметь нестандартные формы, например, ниша в спальне или встроенный шкаф. Стоит заметить, что способ найти площадь нестандартного пола все же можно. Для этого необходимо разбить помещение на небольшие геометрические фигуры, например, треугольники, квадраты, прямоугольники и т. д. Конечно, есть множество других способов, как рассчитать площадь пола, но с помощью такого способа — это сделать намного проще.

После того, как помещение будет разделено на геометрические фигуры, можно легко узнать их площадь, перемножив стороны одну на другую. После всех расчетов, площади фигур необходимо сложить, таким образом можно узнать точную площадь.

Как вычислить площадь помещения, в котором есть скошенные углы?

Вычислить площадь помещения, в котором есть скошенный угол — достаточно просто, для этого нужно:

• Вычислить стороны треугольника;
• Рассчитать площадь по формуле S = (a*b)/2. В этом случае a и b — катеты треугольника.

Формула Герона.

Калькулятор расчета площади

Существует множество способов как найти площадь пола, одним из них является онлайн калькулятор, который позволит быстро и надежно рассчитать площадь любого помещения. От вас только требуется внести замеры в специальную таблицу.

Преимущества калькулятора расчета площади:

• Возможность высчитать площадь любой геометрической фигуры;
• Нет необходимости самостоятельно просчитывать;
• Скорость и точность расчетов.

Калькулятор расчета площади — это оптимальное решение вопроса, как быстро посчитать площадь пола комнаты.

Как посчитать необходимое количество плитки

Для того, чтобы узнать необходимое количество плитки, необходимой для укладки в той или иной комнате, необходимо узнать площадь помещения. Как быстро найти площадь пола любой комнаты — описано выше. После того, как площадь будет рассчитана, необходимо узнать площадь 1 плитки из выбранной коллекции. После этого нужно просчитать, сколько плиток необходимо для укладки её в комнате.

• Площадь комнаты: 20 м2;
• Размеры плитки: 0,2 х 0,4 м;
• Площадь 1 плитки: 0,08 м2;
• Необходимое количество плиток: 250.

Таким способом можно узнать количество необходимой плитки. Таким же способом можно рассчитать необходимое количество паркетной доски или ламината. Стоит заметить, что в некоторых случаях количество необходимых материалов зависит от узора, который будет выполнен на напольной поверхности.

Данные по площади пола можно узнать из домовой книги. Комнаты, которые имеют сложную геометрическую форму проще всего рассчитывать с помощью деления их на небольшие геометрические объекты.

Узнать площадь полукруглой поверхности можно с помощью формулы: S = πR2/2 — радиус круга.

Для того, чтобы напольный материал не пришлось покупать еще — добавьте до необходимого количества 10%. Если вы правильно вычислите необходимое количество материалов — вы сможете качественно и надежно уложить любое напольное покрытие.

3 9 710 0

Чаще всего этот вопрос актуален тем, кому в ближайшем времени предстоит делать ремонт. От квадратных метров комнаты или квартиры зависит количество необходимых стройматериалов. Стоимость роботы мастеров ремонта тоже зависит от квадратуры. Поэтому, научиться самому рассчитывать квадратные метры жилья очень важно. Мы поделимся с вами некоторыми способами как это правильно делать. Учитывая наши советы вы легко и очень быстро научитесь делать это самостоятельно.

• Рулетку лучше использовать с большим запасом метровой ленты. Например, 10-метровую. Это намного удобнее. Но если в наличии есть инструмент меньшей длинны, не обязательно искать ему замену. Вам придется только чаще переставлять его. Главное – не упустите точку, где метраж заканчивается.
• Возможно, вам потребуется помощь. Рулетку нужно придерживать или как-то закреплять в начальной и следующих точках.
• Проводить рулеткой необходимо по максимально ровной линии. Иначе расчеты могут быть больше. Как следствие – неправильно вычисленная квадратура комнаты.
• Периметр стен отмеряйте вместе с окнами и дверью. Потом, отдельно подсчитав их размеры, отнимите от общего периметра и получите квадратуру помещения. Это быстрее и удобнее, чем маленькими частями отмерять комнату.

Начало рулетки поместите в один из углов комнаты (А). Она должна быть там зафиксирована. Плотно прижимая к стене, растягиваете 10-метровую ленту (зависит от вашей рулетки), протягиваете ко второму углу комнаты (В). Здесь тоже фиксируете рулетку или попросите кого-то придерживать. Протягиваете рулетку в следующий угол комнаты (С).

Получается, вы измеряли ширину и длину помещения. Цифру, которая вышла, умножаете на 2.

Например: 9 метров * 2 = 18 м – общий периметр стен комнаты.

Следующий этап – высота стен. Отмеряем рулеткой от потолка (A) к полу (B). Полученную цифру умножаем на периметр стен.

Например: Высота стен 3 метра. 3 м * 18 м = 54 м – общая площадь по периметру без вычитания оконных отверстий, дверей.

Если в комнате несколько окон одинакового размера, достаточно отмерить только одно окно. Рулеткой отмеряем ширину (A-B) и высоту (B-C) оконных откосов. Умножаем обе цифры.

Например: 2 м (ширина окна) * 1,8 м (высота окна) = 3,6 м – периметр окна.

Если окна разные, отмеряем периметр каждого отдельно.

То же самое проделываем с дверью. Отмеряем, потом умножаем ширину дверей (А-В) на высоту (В-С).

Например: 0,8 (ширина дверей) * 2 м (высота дверей) = 1,6 м – периметр дверей.

Точный расчет квадратных метров требуется в основном при ремонте дома или квартиры. По полученному результату вы очень легко купите именно то количество обоев или плитки, которые требуются для того или иного помещения.

Как посчитать метры квадратные – необходимые инструменты

Вам потребуются:

• Специальная строительная рулетка или длинная, не менее 1 м, линейка.
• Простой карандаш для отметок на стенах, потолках и полах.
• Тетрадь для записей и шариковая ручка.
• Калькулятор.

Как посчитать метры квадратные – основная формула

Из школьной программы вы наверняка помните, что любая площадь, которая измеряется в квадратных метрах, вычисляется путем перемножения всего двух величин: ширины и длины.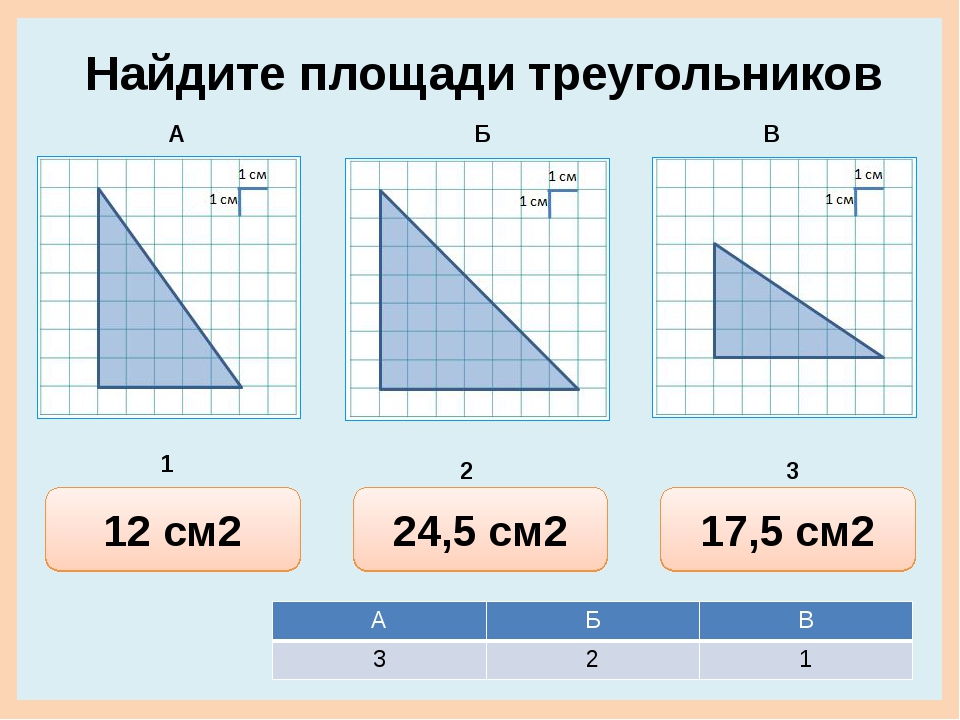

где: S – площадь (кв.м), a – длина (м), b – ширина (м).

Обозначения в этой формуле применимы для горизонтальных поверхностей, т.е. пола и потолка. Для вертикальных же стен формула выглядит так?

где: S – площадь (кв.м), a – длина стены вдоль плинтуса (м), h – высота стены от пола до потолка.

Как посчитать метры квадратные потолка или пола

Самым простым является расчет квадратных метров сплошных горизонтальных поверхностей – т.е пола и потолка. Так как потолок является зеркальным отражением пола, то определив площадь пола вы с уверенностью можете утверждать, что и потолок имеет такое же количество квадратных метров. Итак:

• Возьмите в руки рулетку и зафиксируйте ее кончик в углу комнаты возле самого пола. Протяните рулетку вдоль всей стены до следующего угла и запишите в тетрадь полученную цифру (например, 6 м). Если вместо длинной рулетки вы будете пользоваться линейкой, то после каждого перекладывания линейки делайте пометки на полу. Полученные 6 метров – это длина (a).
• Таким же образом измерьте ширину (b) пола. Например, она у вас получится 4 м. Запишите это значение в тетрадь.
• Возьмите калькулятор и перемножьте длину на ширину: 6*4. Результат 24 и будет количеством квадратных метров пола или потолка.

Как посчитать квадратные метры сплошной стены

С помощью рулетки или линейки измерьте длину стены вдоль плинтуса. Например, она составит 5 м. Далее измерьте высоту стены – лучше всего это делать по углу. Допустим, высота комнаты у вас получилась 3,3 м. Теперь перемножьте эти две величины: 5*3,3 = 16,5. Результат 16,5 и будет теми самыми квадратными метрами.

Как посчитать квадратные метры стены с окном

Для расчета вам потребуются дополнительные измерения окна и стандартные измерения стены.

• Измерьте высоту окна и его ширину. Например, высота у вас получится 1 м, а ширина – 1,5 м. Перемножьте эти две величины: 1*1,5 = 1,5 квадратных метров (площадь окна).
• Измерьте длину стены вдоль плинтуса (возьмем те же 5 м) и высоту стены (возьмем те же 3,3 м). При перемножении получите 16,5 квадратных метров.
• Из общего количества квадратных метров стены (это 16,5) отнимите количество квадратных метров окна (это 1,5). Результатом станет 15 квадратных метров (16,5-1,5).

Как посчитать квадратные метры стены с дверью

Расчет производите аналогично расчету квадратных метров стены с окном.

Зная точные значения квадратных метров, вы можете идти в магазин и покупать обои или плитку для ремонта. Обязательно обратитесь к консультанту и покажите ему все измерения и расчеты. Дело в том, что все отделочные материалы необходимо приобретать с учетом подбора рисунка или резки плитки – запас по квадратным метрам может составлять от 10 до 20 %.

Главная » Стены » Как посчитать площадь листа. Как узнать площадь комнаты? Измерение площади прямоугольных помещений

Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора

Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.

Треугольник
Площадь = ½ × b × h
b = основание
h = высота по вертикали Квадрат
Площадь = a ²
a = длина стороны Круг
Площадь = π × r ²
r = радиус Сектор
Площадь = ½ × r ² × θ
r = радиус
θ = угол в радианах

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = w × h
w = ширина
h = высота

Мы знаем, что w = 5 и h = 3 , поэтому:

Площадь = 5 × 3 = 15

Пример: Какова площадь этого круга?

Радиус = r = 3

Площадь		= π × r 2
		= π × 3 2
		= π × (3 × 3)
		= 3. 14159 … × 9
		= 28,27 (до 2 знаков после запятой)

Пример: Какова площадь этого треугольника?

Высота = h = 12

База = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Более сложный пример:

Пример: Сэм косит траву по цене 0 долларов.10 штук за квадратный метр

Сколько зарабатывает Сэм, обрабатывая эту область:

Разобьем область на две части:

Часть А представляет собой квадрат:

Площадь A = a ² = 20 м × 20 м = 400 м ²

Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итак, общая площадь:

Площадь = Площадь A + Площадь B = 400 м ² + 140 м ² = 540 м ²

Сэм зарабатывает 0 долларов. 10 штук за квадратный метр

Сэм зарабатывает = 0,10 доллара × 540 млн ² = 54 доллара

1754, 1755, 1756, 1757, 1758, 1759, 1760, 1761, 3250, 3251

Калькулятор площади с использованием карт

Этот планиметр можно использовать для измерения замкнутой области определенной полилинии на карте.

[11 июля 2018] К сожалению, из-за значительного повышения цен на серверные услуги мы больше не можем предлагать некоторые функции на этой странице.

Инструкции

Для использования калькулятора площади:

• Масштабируйте и перемещайте карту, чтобы найти интересующую область
• Щелкните карту, чтобы разместить вершины ломаной линии
• Щелкните столько раз, сколько необходимо, чтобы определить полилинию

Огражденная площадь будет выводиться в квадратных метрах и квадратных километрах

Вы можете нажать кнопку [Удалить последнюю точку], если вы допустили ошибку, или нажать [Очистить все] точки, чтобы удалить все точки с карты и начать заново.

Вы также можете изменить положение маркеров после того, как они были размещены на карте, перетащив их.

Чтобы нарисовать новую область, нажмите кнопку [Начать новую область] или нажмите Alt + n

Информация

Инструмент калькулятора площади позволяет определить площадь, заключенную внутри замкнутой полилинии, наложенной на карту.

Ориентиры

Измерение озера Лох-Ней в Северной Ирландии. Сообщается, что площадь озера Лох-Ней составляет 388 км² [1], так что значение 380 823 442 м² не за горами.

Будущее использования и идеи

• Разрешить пользователю изменять цвет полилиний и заливку области (включая прозрачную)
• Разрешить сохранение области для дальнейшего использования
• Вариант экспорта в KML

История версий

• 17 июня 2015 — Маркеры теперь показывают широту и долготу при наведении на них курсора
• 18 декабря 2014 — Подсчитана общая площадь
• 23 марта 2014 г. — Добавлен выход гектаров
• 6 августа 2013 г. — Исправлена ​​проблема с выводом периметра
• 21 февраля 2013 — Добавлен результат в квадратных футах
• 8 января 2012 г. — обновление до Google Maps API V3 и некоторые новые функции
• 20 июля 2010 — Добавлены перекрестия и возможность включения / выключения перекрестия
• 17 июня 2010 г. — добавлена ​​опция загрузки KML (бета)
• 2 июня 2010 г. — элемент управления масштабом перемещен в верхнюю часть карты, чтобы избежать конфликта с панелью поиска Google.
• 2 февраля 2010 г. — Добавлен вывод периметра в метрах и километрах
• 25 марта 2008 г. — добавлены перетаскиваемые маркеры, возможность щелкать внутри многоугольника и выводить данные в акрах
• 26 июня 2007 г. — добавлен расчет базовой площади
• 24 июня 2007 — Страница создана

Как найти площадь прямоугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Что такое площадь? — Определение, факты и пример

Area Games

Area

Используйте единичные квадраты, чтобы понять концепцию площади и найти площадь для различных двухмерных форм.

охватывает Common Core Curriculum 3.MD.7Играть сейчасПосмотреть все игры по геометрии >>

Учитесь с полной программой обучения математике K-5

Что такое область? В геометрии площадь может быть определена как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.

Площадь приведенных ниже квадратов со стороной 1 сантиметр каждый будет измеряться в квадратных сантиметрах (см²).

Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).

Слово «площадь» происходит от латинского «площадь», что означает свободный участок ровной поверхности. Происхождение далее привело к неправильному получению площади как «определенного количества пространства, заключенного в пределах набора границ».

Мы часто находим площадь пола комнаты, чтобы определить размер покупаемого ковра. Покрытие пола плиткой, покрытие стен краской или обоями или строительство бассейна — это другие примеры, когда площадь вычисляется.

Обычные простые формы и многоугольники имеют свои собственные формулы для вычисления площади. Вот как вычисляется площадь обычных двухмерных или двумерных фигур:

Двумерные геометрические формы:

Название формы:	Изображение формы:	Формула площади:
Круг		Площадь = πr², где r радиус.
Треугольник		Площадь = bh, , где b — основание, А h — высота.
Квадрат		Площадь = l × l, где l — длина каждой стороны.
Прямоугольник		Площадь = длина × ширина, где l длина и w — ширина.
Параллелограмм		Площадь = b × h, , где b — основание, , а h — высота по перпендикуляру.
Трапеция		Площадь = (a + b) h, , где a и b — длины параллельных сторон, , а h — высота по перпендикуляру.

В реальной жизни не каждую плоскую фигуру можно однозначно классифицировать как прямоугольник, квадрат или треугольник. Чтобы найти площадь составной фигуры, состоящей из более чем одной фигуры, нам нужно найти сумму площадей обеих или всех фигур, образующих составную фигуру.

Площадь внешней поверхности твердой или трехмерной формы называется площадью поверхности. Например, прямоугольная призма имеет 6 прямоугольных оснований и боковые грани.Итак, общая площадь поверхности — это сумма площадей всех 6 прямоугольников.

Интересные факты Среди всех фигур с одинаковым периметром круг имеет наибольшую площадь.

Давайте споем!

Для посадки овощей в саду,

Найдите площадь поля — все внутри.

Умножьте его длину на ширину,

И вот формула площади, которую вы применили!

Давайте сделаем это!

Вместо того, чтобы раздавать детям рабочие листы по математике, вовлекайте их в проекты по благоустройству дома.Сообщите им о комнате, которую вы собираетесь покрасить. Попросите их подсчитать общую площадь поверхности стен, чтобы узнать, сколько требуется краски.

Обсудите, как все стены в комнате могут отличаться друг от друга, и, таким образом, измерение общих размеров с последующим вычитанием площади двери, окон или книжных полок поможет оценить необходимое количество краски.

Вы также можете попросить рассмотреть возможность определения общей площади подарка, который они упаковывают, чтобы определить необходимое количество оберточной бумаги.

Сопутствующая математическая лексика

Площадь прямоугольника — формула, определение, примеры

Площадь любой формы — это количество единичных квадратов, которые могут в нее поместиться. Здесь «единица» относится к единице (1), а единичный квадрат — это квадрат со стороной, равной 1 единице. Итак, площадь прямоугольника — это количество единичных квадратов внутри границы прямоугольника. В качестве альтернативы пространство, занимаемое по периметру прямоугольника, называется площадью прямоугольника.Хорошим примером прямоугольной формы являются квадратные плитки единичной длины в вашем доме. Вы легко сможете определить, сколько места занимает пол, посчитав количество плиток. Это также поможет вам определить площадь прямоугольного пола.

Что такое площадь прямоугольника?

Площадь можно определить как количество пространства, занимаемого плоской поверхностью определенной формы. Он измеряется в «количестве» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. Д.).) Площадь прямоугольника — это количество единичных квадратов, которые могут уместиться в прямоугольник. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов портативных компьютеров, школьные доски, холсты для рисования и т. Д. Вы можете использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма.

Площадь прямоугольника Определение: Площадь, занимаемая прямоугольником в пределах его границ, называется площадью прямоугольника.

Нарисуем внутри прямоугольника единичные квадраты. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм.

Теперь посчитайте количество единичных квадратов на рисунке выше. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже узнали, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника — дюймы, площадь измеряется и записывается в квадратных дюймах. Таким образом, площадь вышеуказанного прямоугольника = 12 квадратных дюймов.

Формула площади прямоугольника

Формула площади прямоугольника используется для определения площади, занимаемой прямоугольником в пределах его границ. В приведенном выше примере площадь прямоугольника, длина которого составляет 4 дюйма, а ширина 3 дюйма, составляет 12 квадратных дюймов. У нас 4 × 3 = 12. Площадь прямоугольника получается умножением его длины и ширины. Таким образом, формула для площади «A» прямоугольника, длина и ширина которого равны «l» и «w» соответственно, представляет собой произведение « l × w ».

Площадь прямоугольника = (длина × ширина) квадратных единиц

Как рассчитать площадь прямоугольника?

Площадь прямоугольника равна его длине, умноженной на ширину. Следуйте инструкциям ниже, чтобы найти площадь прямоугольника.

• Шаг 1 : Обратите внимание на размеры длины и ширины из приведенных данных.
• Шаг 2 : Найдите произведение значений длины и ширины.
• Шаг 3 : Ответьте в квадратных единицах.

Давайте рассмотрим пример, чтобы понять расчет площади прямоугольника. Найдем площадь прямоугольника, длина которого составляет 15 единиц, а ширина — 4 единицы. Чтобы найти площадь, сначала найдите длину и ширину.

Дано, длина = 15 единиц и ширина = 4 единицы

Формула для определения площади прямоугольника: A = l × w. Замените 15 вместо l и 4 вместо w в этой формуле. Площадь прямоугольника = 15 × 4 = 60.

Следовательно, площадь прямоугольника = 60 квадратных единиц

Площадь прямоугольника по диагонали

Диагональ прямоугольника — это прямая линия в прямоугольнике, соединяющая его противоположные вершины.В прямоугольнике две диагонали и обе одинаковой длины. Мы можем найти диагональ прямоугольника, используя теорему Пифагора.

(диагональ) ² = (длина) ² + (ширина) ²

(длина) ² = (диагональ) ² — (ширина) ²

Длина = ⎷ (диагональ) ² — (ширина) ²

Теперь формула для вычисления площади прямоугольника — длина × ширина. В качестве альтернативы мы можем записать этот продукт как (⎷ (Диагональ) ² — (Ширина) ² ) × Ширина

Итак, площадь прямоугольника = ширина (⎷ (диагональ) ² — (ширина) ² )

Почему площадь прямоугольника равна длине × ширине?

Вы когда-нибудь задумывались, почему формула для определения площади прямоугольника равна длине × ширине? Выведем формулу площади прямоугольника. В прямоугольнике ABCD нарисуем диагональ AC.Ясно, что диагональ AC делит прямоугольник ABCD на два равных треугольника. Площадь прямоугольника равна сумме площадей этих двух треугольников.

Площадь прямоугольника ABCD = Площадь треугольника ABC + Площадь треугольника ADC

= 2 × Площадь треугольника ABC

= 2 × (1/2 × основание × высота)

= AB × BC

= длина × ширина

Часто задаваемые вопросы о площади прямоугольника

Какова площадь прямоугольника в геометрии?

Площадь пространства, занимаемого по периметру прямоугольника, называется площадью прямоугольника. Он рассчитывается путем нахождения произведения длины и ширины прямоугольника.

Каков периметр и площадь прямоугольника?

Периметр прямоугольника равен сумме его четырех сторон. Следовательно, периметр прямоугольника = 2 единицы (длина + ширина). Площадь прямоугольника определяется как произведение длины и ширины. Выражается в квадратных единицах.

Какова формула площади прямоугольника?

Площадь прямоугольника (A) равна произведению его длины «a» и ширины или ширины «b».Итак, площадь прямоугольника = (a × b) квадратных единиц.

Что такое единица площади прямоугольника?

Единица площади прямоугольника — квадратные единицы. Например, если размеры прямоугольника 4 дюйма × 3 дюйма. Площадь прямоугольника 12 квадратных дюймов.

Почему мы вычисляем площадь прямоугольника?

Мы вычисляем площадь прямоугольника, чтобы найти площадь, занимаемую прямоугольником в пределах его периметра.

Как определить площадь прямоугольника по его диагонали?

Мы можем найти диагональ прямоугольника, используя теорему Пифагора: (Диагональ) ² = (Длина) ² + (Ширина) ² . Теперь формула для вычисления площади прямоугольника — длина × ширина. В качестве альтернативы мы можем записать этот продукт как (⎷ (Диагональ) ² — (Ширина) ² ) × Ширина

Площадь прямоугольника такая же, как и площадь квадрата?

Нет, площадь квадрата не обязательно совпадает с площадью прямоугольника, потому что каждый квадрат представляет собой прямоугольник с равной длиной и шириной, но все прямоугольники не квадратные. Формула для вычисления площади прямоугольника — длина × ширина, а площадь квадрата — (сторона) ² .

Формулы площади

( пи = = 3,141592 …)

Площадь Формулы

Примечание: «ab» означает «а» умножить на «б». «a

² » означает «квадрат», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений.

Примеры

квадрат = a ²

прямоугольник = ab

параллелограмм = bh

трапеция = h / 2 (b ₁ + b ₂ )

03 круг

=

03 круг

=

pi r ²

эллипс = pi r ₁ r ₂

треугольник =

, равная половине длины основания, умноженной на высоту треугольник

равносторонний треугольник =

треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C

треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)

правильный многоугольник = (1/2) n sin (360 ° / n) S ²
когда n = количество сторон и S = ​​длина от центра до угла

Шт.

Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.

Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.

Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам, умноженным на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в ² .)

Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.

Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?

НЕ ПРАВИЛЬНО …. 4 раза 6 = 24

ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута ² ).

Площадь неправильных форм — расчет, примеры и часто задаваемые вопросы

Неправильные формы — это многоугольники с пятью или более сторонами различной длины. Эти формы или фигуры могут быть дополнительно разложены на известные формы, такие как треугольники, квадраты и четырехугольники, чтобы оценить площадь.

Вот некоторые примеры неправильной формы:

Объекты повседневной жизни неправильной формы

Как рассчитать площадь неправильной формы?

Определение площади неправильной формы

Существуют различные методы оценки площади неправильной формы:

• Оценка площади с использованием единичных квадратов.

• Разделение неправильной формы на две или более правильных формы.

• Разделение неправильной формы кривыми на две или более правильных формы.

Как найти область неровной формы?

Оценка площади с помощью единичных квадратов

Мы можем использовать этот метод для фигур с кривыми, отличными от идеального круга или полукругов и неправильных четырехугольников. В этом методе мы сначала делим фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в форму, используется для определения общей площади.

Например: Рассчитайте площадь, посчитав единичные квадраты на приведенном ниже рисунке.

Ответ: Если обозначить каждую единицу квадрата в сантиметрах, площадь будет равна 6 см ² .

Расчет площади неправильной формы с изогнутыми краями

Разделение неправильной формы на две или более правильных формы

Используйте этот метод для расчета площади неправильной формы, которая представляет собой комбинацию треугольников и многоугольников.Используя предопределенные формулы, вычислите площадь таких фигур и сложите их, чтобы получить общую площадь.

Например, в приведенной ниже неправильной форме мы разделим несколько ребер на треугольник и три многоугольника.

Общую площадь фигуры можно рассчитать, добавив отдельные площади:

Общая площадь = Площадь (ABIM) + Площадь (BCGH) + Площадь (CDEF) + Площадь (JKL)

⇒ Общая площадь = (AB × BI ) + (BC × CG) + (CD × DE) + (12 × LJ × KO)

⇒ Общая площадь = (10 × 5) + (3 × 3) + (2 × 2) + (1⁄2 × 4 × 4)

⇒ Общая площадь = 50 + 9 + 4 + 8

⇒ Общая площадь = 71 см ²

Расчет площади неправильной формы

Для расчета площади неправильной формы разделите форму на кривые в две или более правильные формы.

В этом методе разделите неправильную форму на несколько квадратов, треугольников или других четырехугольников. В зависимости от формы или кривых, часть фигуры может быть кругом, полукругом или квадрантом.

Найдите участки неправильной формы с 8 сторонами, включая одну кривую.

Sol: Мы определим неизвестные количества по заданным размерам сторон. Для начала нам нужно разделить фигуру на два прямоугольника и полукруг.

Площадь фигуры ABCDEF составляет:

Общая площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)

Общая площадь = (AB × AG) + (GD × DE) + ( 1⁄2 × π × ob ² )

Общая площадь = (3 × 4) + (10 × 4) + (1⁄2 × 3.14 × 12)

Общая площадь = 12 + 40 + 1,57

Следовательно, общая площадь = 53,57 см ²

Как найти площадь неправильной формы с помощью миллиметровой бумаги?

Какова площадь неровной поверхности?

Найдите площадь данного листа.

Решение: Чтобы найти площадь неровной поверхности в листе вышеупомянутого случая, мы должны положить лист на миллиметровую бумагу и нарисовать его границу.

Форма листа неправильная.Таким образом, мы предположим, что более половины площади, покрытой листом, будет считаться за 1, а меньшее — за 0.

Теперь посчитайте количество полностью закрытых фигур. Полностью покрыто 64 квадрата.

Также посчитайте частично покрытые более чем половиной квадраты, и каждый будет считать qs 1 квадрат. Есть 17 кв. Больше половины кв.

Кроме того, посчитайте частично менее чем половину закрытого квадрата, и каждый будет засчитан как 0.Есть 16 квадратов меньше половины квадрата.

Теперь сложите все квадраты, чтобы найти площадь листа = 64 + 17 x 1 + 16 x 0 = 64 + 17 = 81 квадратную единицу.

Следовательно, площадь створки составит 81 кв.

Формула площади неправильных форм

Чтобы найти площадь неправильных форм, во-первых, нам нужно разделить неправильную форму на правильные формы, которые вы можете распознать, такие как треугольники, прямоугольники, круги, квадраты и так далее.

Затем найдите площадь этих отдельных форм и сложите их, чтобы получить область неправильных форм.

Решенный пример

В. Найти площадь данной формы?

Sol: Рисунок выше имеет три правильные формы. Начинайте деление сверху, у него есть треугольник, прямоугольник и трапеция.

Мы найдем площадь для каждой из этих трех фигур и сложим результаты, чтобы получить окончательную площадь фигуры.

Треугольник

Площадь треугольника = (основание × высота) / 2

= (3 × 4) / 2

= 12/2

= 6

Прямоугольник

Площадь прямоугольника = длина × ширина

= 3 × 10

= 30

Трапеция

Площадь трапеции = ((b ₁ + b ₂ ) × h) / 2

= ((3 + 5) × 2) / 2

= (8) × 2/2

= 16/2

= 8

Следовательно, площадь данной формы = 6 + 30 + 8 = 44.