Площадь умножить на высоту: Площади фигур — Сайт учителя математики

09.05.2021 автор alexxlab

Содержание

Площади фигур — Сайт учителя математики

Площади многоугольников
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.

С понятием площади нам приходиться сталкиваться ежедневно. Для того, чтобы постелить новую плитку в вашей квартире вам нужно приобрести определенное ее количество, которое будет зависеть от площади вашей комнаты. Размер земельного участка вашего дома также будет характеризоваться площадью. Обычно люди забывают как найти площадь более сложных фигур, таких как треугольник, трапеция, или круг, но если вы настолько закрутились в жизни, что забыли как найти площадь прямоугольника, то мы вам это напомним в данной статье.

Вычисление площади прямоугольника.

Площадь измеряют в квадратных единицах, миллиметрах, сантиметрах, метрах и так далее. Сколько квадратов в данном прямоугольнике?

Совершенно верно. В нем пятнадцать квадратных единиц. Значит для того, чтобы найти площадь прямоугольника нужно его ширину умножить на длину. В виде формулы это можно представить как S = h*b, где S-площадь, h-высота, b-ширина. Или так:
площадь прямоугольника = ширина х длину.
Вот еще несколько примеров определения площади прямоугольника.

	Площадь = Длина х Ширина Площадь = 9 х 5 = 45 квадратных единиц
	Площадь = Длина х Ширина Площадь = 8 х 6 = 48 квадратных единиц

Единицы измерения площади.
Как было сказано выше площадь измеряется в квадратных единицах. Они будут различными в зависимости от размера измеряемой площади. Конечно, можно измерять все в одних единицах, но в результате мы будем получать либо слишком маленькие, либо слишком большие для восприятия цифры.

Пример	Единица измерения	Единица площади
Ноготь на пальце	Миллиметр	мм²
Лист бумаги	Сантиметр	см²
Комната	Метр	м²
Город	Километр	км²

Площадь земельных участков еще часто указывают в сотках. Одна сотка — это площадь участка размером 10х10 метров, которая составляет 100 квадратных метров и поэтому называется соткой. Вот несколько характерных примеров размеров, которые может иметь земельный участок площадью 15 соток.

Ширина 15, длина 100	Площадь 1500 м²	Площадь 15 соток
Ширина 20, длина 75	Площадь 1500 м²	Площадь 15 соток
Ширина 25, длина 60	Площадь 1500 м²	Площадь 15 соток
ширина 30, длина 50	Площадь 1500 м²	Площадь 15 соток

В будущем, если вы вдруг забудете как найти площадь прямоугольника, то вспоминайте очень старый анекдот, когда дедушка спрашивает у пятиклассника как найти площадь Ленина, а тот отвечает что нужно ширину Ленина умножить на длину Ленина.

Иногда в быту людям приходится вспоминать давно забытые школьные знания. Например, когда при очередном ремонте в доме или квартире нужно определить количество материала для какой-то поверхности треугольной формы. Когда-то вы знали это на зубок, но теперь судорожно пытаетесь вспомнить как найти площадь треугольника?

Не переживайте! Это нормально, когда человеческий мозг перекладывает уже давно не используемую информацию в удаленные уголки, из которых ее не вседа получается быстро извлечь. А чтобы вы не мучились этим вопросом, мы напомним как найти площадь треугольника различными методами в данной статье.

Как известно, треугольником называется плоская фигура, образованная пересекающимися прямыми. Точки пересечения называют вершинами, а противоположные им отрезки прямых ребрами. Встречаются частные виды треугольников, такие как прямоугольный, равнобедренный и равносторонний треугольники.

С самом общем случае площадь треугольника находится как половина произведения длина основания треугольника на величину высоты, опущенной на данное основание с противоположной вершины. Записывается это следующим образом S = 1/2*b*h, где S-площадь треугольника, b-длина одной из сторон треугольника, h-высота, опущенная к этой стороне.

Данную формулу можно хорошо понять, запомнить и вспоминать по частному случаю нахождения площади прямоугольного треугольника. Посмотрите внимательно на рисунок.

Как видите площадь такого треугольника легко определяется как половина площади воображаемого прямоугольника образованного из двух таких треугольников. Для непрямоугольного треугольника вы как бы добавляете два треугольника до образования прямоугольника и находите его площадь.
Если известна длина трех сторон треугольника, то его площадь может быть найдена по формуле Герона. Для упрощения ее использования вводят новую величину, называемую полупериметром, который находиться как половина суммы всех сторон треугольника и записывается в виде P = (a+b+c)/2, где P-полупериметр, а,b,с-стороны (ребра) треугольника. После нахождения полупериметра формула Герона принимает следующий вид: S = √(p(p-a)(p-b)(p-c)), где S — площадь треугольника, √-квадратный корень, p-полупериметр, a,b,c-стороны (ребра) треугольника.

Существуют также другие формулы того, как найти площадь треугольника, но мы не станем их здесь приводить, так как в них используются такие данные как синусы углов и которые больше подходят для задач по математической практике, чем по бытовому использованию.

Как найти площадь трапеции? Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.

Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

Средняя линия трапеции равна полусумме оснований и параллельна им.
У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.

Как найти площадь трапеции.
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается как S = ((a+b)*h)/2, где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.

Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.

Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле: S = ((a+b)/2)*√c²-((b-a)²+c²-d²/2(b-a))², где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.

Мы знаем, что окружность представляет собой множество точек равноудаленных от заданной точки и лежащих с данной точкой, а также между собой в одной плоскости. Точка, от которой равноудалены другие точки называется центром окружности.

Расстояние от любой точки окружности до его центра называется радиусом окружности и обычно обозначается заглавной английской буквой R.
Расстояние между двумя противолежащими точками, у которых соединяющий их отрезок проходит через центр окружности, называется диаметром окружности и по общепринятым стандартам обозначается английской заглавной буквой D.

Кругом называется часть плосткости, ограниченная окружностью.

Исходя из определения окружности можно понять, что диаметр равен двум радиусм окружности D=2R, а радиус наоборот равен половине диаметра R=D/2.

После того, как были определены все свойства и ключевые характеристики кругов и окружностей можно приступить к определению площади круга, для чего может быть использована следующая формула:

S = πR²

где, S — площадь круга, π — число пи (о нем мы расскажем ниже), R — радиус окружности.

π=3,14.

Формулу площади круга можно преобразовать с учетом того, что радиус равен полудиаметру круга. В этом случае она примет вид:

D = πD²/4

где, S — площадь круга, π — число пи, D — диаметр окружности.

Объем комнаты и площадь пола

Вот такая вот интересная задачка:

Объем комнаты 75 метров кубических, высота комнаты 3 метра. Найдите площадь пола.

Решение задачи тупо:

75 : 3 = 25 (метров квадратных)

Если объем комнаты разделить на её высоту, то получится площадь пола. Если в вашей задаче написано «объем комнаты 75 метров квадратных…», то значит эту задачу составляло туловище, которое ни фига не понимает в единицах измерения объемов. Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.

А теперь бла-бла-бла на заданную тему.

Ничего сложного в этой задаче нет, просто вместо обычного прямоугольного параллелепипеда здесь нам рассказывают о комнате. В переводе на язык математики и применительно к параллелепипеду эта задача будет звучать так:

Объем прямоугольного параллелепипеда равен 75 кубических метров, его высота равна 3 метра. Найдите площадь основания этого прямоугольного параллелепипеда.

В чём маленький подвох, который многих может сбить с толку? Дело в том, что комнату мы привыкли видеть изнутри.

Высота комнаты и площадь пола

Эта комната изображена на стадии ремонта. После ремонта можете обставить её мебелью по своему вкусу.

Кстати, большинство людей вспоминают про геометрию именно после начала ремонта — площади, периметры, объемы… Так вот, математики нам показывают прямоугольные параллелепипеды всегда снаружи.

Прямоугольный параллелепипед с обозначениями

Если в математике мы привыкли видеть любой объем снаружи, то попадая внутрь реального объема очень легко растеряться.

Теперь разберемся с названиями. То, что в комнате называется «объем комнаты», в математике называется просто «объем». «Высота комнаты» в математике будет просто «высота», а «площадь пола» — это ничто иное, как «площадь основания». Хорошо или плохо, но математики нас учат, что если площадь основания умножить на высоту, то мы получим объем. При решении задачи мы объем разделили на высоту и получили площадь.

Еще один интересный момент. Комната может иметь любую форму с вертикальными стенами. Пол в комнате может быть квадратным, прямоугольным, треугольным, шестиугольным, круглым, бесформенным. .. В любом случае, его площадь будет равна 25 квадратных метров. Ведь любая двухмерная геометрическая фигура может иметь площадь в 25 метров в квадрате. При умножении этой площади на высоту в 3 метра мы всегда будем получать объем в 75 метров кубических.

Является ли подобная задача реальной? Волне. В отдельных бюрократических документах можно встреть объем комнаты. Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему. Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.

P.S. Кстати, на сайте «Русский текст» вы можете найти редкие и уникальные тексты, статьи из старых газет, интересные публикации на русском языке.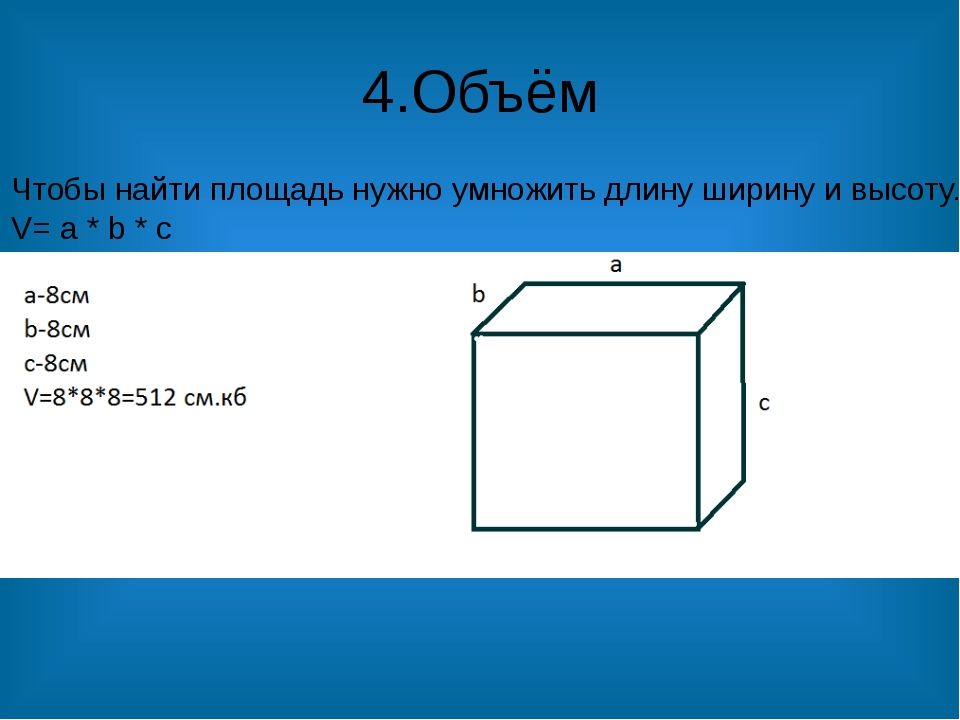 Любознательность ещё никому не навредила. Конечно, если любознательностью попользоваться с умом. Если вы прочтете какую-нибудь старую, давно забытую, но интересную статью о науке — вы станете умнее, чем были до этого.

Формулы объема и площади поверхности. Призма, пирамида

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Ты нашел то, что искал? Поделись с друзьями!

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Рассчитать объем коробки в м3 и литрах онлайн

07.10.2019

Сколько будет стоить отправка вашего груза до места назначения? Чтобы ответить на это вопрос, нужно знать его объем в кубических метрах, т. к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.

Картонные коробки — наиболее выгодный и удобный вид упаковки для большинства товаров. Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.

Если в результате расчета оказалось, что вам требуется гофротара индивидуальных размеров, наша компания «МС-ПАК» изготовит нужный тираж на заказ. Рассмотрим, как правильно рассчитать объем картонной коробки.

Поэтапный расчет объема картонной коробки

Для расчета нужно:

Формула для вычисления объема V в м³ коробки с прямоугольным или квадратным основанием:
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
Если в основании коробки не прямоугольник, а треугольник, пяти- или шестиугольник, то формула вычисления объема будет:
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
Тип: Профиль: Толщина (мм):
Трехслойный гофрокартон B 3
Трехслойный гофрокартон C 3,7
Трехслойный гофрокартон E 1,6
Пятислойный гофрокартон BC 7
Пятислойный гофрокартон BE 4
Перемножив полученные значения, получим объем коробки в кубических метрах.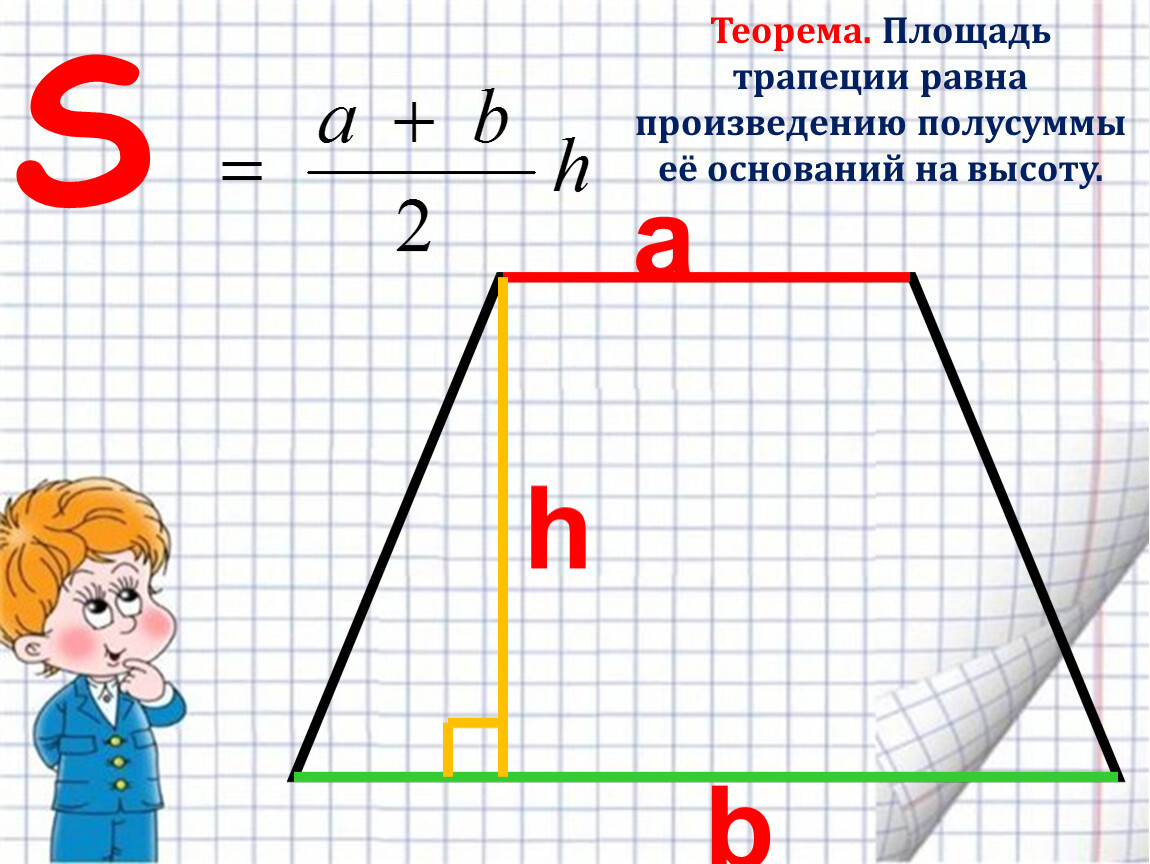 Чтобы получить результат в литрах необходимо полученное значение в м³ умножить на 1000.
Рассчитать объем коробки в м
³ и литрах онлайн
Для обычных коробок в форме куба или параллелепипеда (со сторонами в виде квадратов или прямоугольников) на нашем сайте есть онлайн-калькулятор, который ускорит расчет.
Пример расчета
После измерения получены значения: а=600 мм, b=400 мм, h= 400 мм.
Переводим их в метры: а=600/1000=0,6 м, b=400/1000=0,4 м, h=400/1000=0,4 м.
Подставляя полученные результаты в формулу для расчета объема, получим значение: V=a*b*h=0,6*0,4*0,4=0,096 м³.
Если в коробки фасуются сыпучие или жидкие грузы, то для расчета необходимого объема используем соотношение 1 м³ = 1000 л и, умножив полученное значение объема в м³ на 1000, получим объем в литрах.
Для нашего примера объем коробки (внутренний) в литрах равен 0,096*1000=96 литров.

Дети и учеба — Информационный портал
Зная диагонали, найти высоту ромба легко. В этом нам поможет теорема Пифагора. И хоть она касается прямоугольных треугольников, в ромбе они тоже есть — их образует пересечение двух диагоналей d1 и d2:
Вообразим, что диагональ 1 равна 30 сантиметрам, а диагональ 2 — 40 см.
Итак, наши действия:
Подсчитываем величину стороны по теореме Пифагора. Сторона BC — это гипотенуза (потому что лежит напротив тупого угла) треугольника BXD (X — это пересечение диагоналей d1 и d2). А значит размер этой стороны в квадрате равен сумме квадратов сторон BX и XC. Их размер нам тоже известен (диагонали ромба пересечением делятся пополам) — это 20 и 15 сантиметров. Выходит, что длина стороны BC равняется корню от 20 в квадрате и 15 в квадрате. Сумма квадратов диагоналей равняется 625, а если извлечь это число из корня, получаем размер катета, равный 25 сантиметрам.
Вычисляем площадь ромба при помощи двух диагоналей. Для этого умножаем d1 на d2 и делим результат на 2. Получается: 30 умножить на 40 (= 1200) и поделить на 2 — выходит 600 см кв. — это и есть площадь ромба.
Теперь вычисляем высоту, зная длину стороны и площадь ромба. Для этого нужно площадь поделить на длину катета (это и есть формула вычисления высоты ромба): 1200 делим на 25 — выходит 48 сантиметров. Это окончательный ответ.
Как найти высоту ромба, если известна площадь и периметр (какая формула)?
Ознакомьтесь со всеми формулами расчета площади ромба:
Чтобы узнать высоту, нам нужна самая первая формула (Площадь = Высота умножить на Длину стороны).
Допустим, что периметр равен 124 см, а площадь — 155 см кв.
Нам играет на руку то, что у ромба все стороны одинаковые, потому его периметр — это 4 умножить на длину одного катета.
Найдем длину стороны ромба через известный периметр. Для этого значение периметра (124) делим на 4, и получаем значение 31 сантиметр — длина катета.
Подсчитываем высоту через формулу площади. Делим площадь (155 см кв.) на размер катета (31 см) и получаем 5 сантиметров — это размер высоты данной геометрической фигуры.
Как найти высоту ромба, если известна сторона и угол?
Задача кажется сложной, но это не так. Представим, что размер катета ромба равен корню из трех, а угол — 90 градусам.
Чтобы посчитать размер высоты, используем формулу площади ромба (сторона в квадрате умножить на синус угла). Чтобы узнать синус любого градуса, воспользуйтесь в моем ответе. Синус 90 градусов равняется 1, потому найти высоту будет очень просто. Получается, что площадь равна квадрату длины стороны (3) умножить на синус 90 гр. (1), что в итоге дает ответ- 3 см кв.
А потом делим полученную площадь на размер катета: 3 поделить на корень из 3, и получаем высоту ромба — √3.
Как посчитать высоту ромба, если известна сторона и диагональ?
В этой задаче нужно использовать прямоугольный треугольник, который образован пересечением диагоналей.
Допустим, что сторона равна 10 см, а диагональ — 12 см.
Наши действия:
Находим размер половины второй диагонали при помощи теоремы Пифагора. Гипотенуза в нашем случае — это сторона, потому величина половины диагонали будет равна разнице квадрата катета (10 в квадрате) и квадрата половины известной диагонали (6 в квадрате). Выходит, что нужно от 100 отнять 36 — имеем 64 сантиметра. Добываем корень из этого числа и получаем длину половины второй диагонали — 8 см. А полная длина равна 16 сантиметрам.
Подсчитываем площадь ромба при помощи двух диагоналей. Умножаем длину первой диагонали (12 см) на длину второй (16 см) и делим это на 2 — получаем 96 см кв. (это площадь ромба).
Вычисляем высоту, зная размер стороны и площадь. Для этого 96 поделите на 10 — выходит 9,6 сантиметров — это окончательный ответ.
Геометрическая фигура ромб представляет собой вариацию параллелограмма, имеющего равные стороны. Его высотой является часть прямой, проходящая через вершину фигуры и образующая при пересечении с противолежащей стороной угол 90°. Частным случаем ромба является квадрат. Знание свойств ромба, а также верная графическая интерпретация условия задачи позволяют правильно определить высоту фигуры, используя один из допустимых способов.
Нахождение высоты ромба на основании данных о площади фигуры
Перед вами находится ромб. Как известно, для нахождения его площади необходимо перемножить величину стороны на числовое значение высоты, т.е. S = k * H, где
k – значение, определяющее длину стороны фигуры,
H – числовое значение, соответствующее длине высоты ромба.
Данное соотношение позволяет определить высоту фигуры как: H = S/ k (S – площадь ромба, известная по условию задачи или вычисленная ранее, например как половина произведения диагоналей фигуры).
Нахождение высоты ромба через вписанную окружность
Вне зависимости от длины сторон и величины углов ромба в него можно вписать окружность. Центр данной геометрической фигуры будет совпадать с точкой пересечения диагоналей равностороннего параллелограмма. Информация о величине радиуса такой окружности поможет определить высоту ромба, т.к. r = H/2, где:
r – радиус вписанного в ромб круга,
H – искомая высота фигуры.
Из данного соотношения следует, что высота равнобокого параллелограмма соответствует удвоенному радиусу вписанного в этот параллелограмм круга – H = 2r .

Нахождение высоты ромба через величины углов фигуры
Перед вами ромб MNKP, сторона которого MN = NK = KP = PM = m. Через вершину M проведены 2 прямые, каждая из которых образует с противолежащей стороной (NK и KP) перпендикуляр – высоту. Обозначим их как MH и Mh2 соответственно. Рассмотрите треугольник MNH. Он прямоугольный, а значит, зная ∠N и определение тригонометрических функций, вы можете определить и его сторону-высоту ромба: sinN = MH/MN ⇒ MH = MN * sinN, где:
sinN – синус угла при вершине равностороннего параллелограмма (ромба),
MN (m) – величина стороны заданного ромба.
Т.к. углы ромба, лежащие напротив друг друга, равны между собой, то и величина второго перпендикуляра, опущенного из вершины M, также определяется как произведение MN на sinN.
H = m * sinN – высоту такой фигуры как ромб можно определить путем перемножения числового значения длины его стороны на синус угла при его вершине.

Определив длину одной высоты ромба, вы получаете информацию о величине оставшихся трех перпендикуляров фигуры. Данный вывод следует из того, что у ромба все высоты равны между собой.
Ромб — это четырёхугольник, у которого все стороны равны и противоположные стороны параллельны. Это условие упрощает формулы для определения высоты — перпендикуляра, опущенного из угла на одну из сторон. В четырёхугольнике из каждого угла можно опустить высоты на две стороны. Рассмотрим, как находить высоты ромба, как они соотносятся друг с другом.
Как находить высоту ромба
Четырёхугольники — это такие фигуры, у которых могут изменяться углы при неизменных длинах сторон. Поэтому, в отличие от треугольника, мало знать длины сторон четырёхугольника, необходимо указывать ещё и размеры углов или высоту. Например, если углы ромба равны 90°, то получится квадрат. В этом случае высота совпадает со стороной. Рассмотрим, как найти высоту ромба при углах, отличных от прямых.
Определяем величину двух высот ромба, опущенных из одного угла
Имеем ромб ABCD, у которого AB//CD, BC//AD, АВ = ВС = СD = DА = а. Высотой h называется перпендикуляр, опущенный из угла на противоположную сторону. Опустим высоту АН на сторону ВС, а другую высоту АН1 опустим из того же угла на сторону DС.
Тогда высота АН = AB × sin∟B;
Высота Ah2 = AD × sin∟D.
Одно из свойств ромба — равенство противоположных углов, т.е. ∟B = ∟D. Поскольку АВ = AD (все стороны ромба все равны между собой), то высота АН = АН1. Аналогично можно доказать, что две высоты, опущенные из любого угла, равны между собой.
Как соотносятся остальные высоты ромба между собой
Поскольку противоположные стороны параллельны, то сумма углов, примыкающих к одной стороне, равна 180°. Следовательно, синусы всех четырёх углов равны между собой:
sin∟D = sin(180° — ∟D) = sin∟С = sin∟А = sin∟В.
Следовательно, все высоты, опущенные из любого угла ромба, равны между собой, а сторона, угол и высота связаны между собой жёстким соотношением: h = a × sin∟A, где а — длина любой стороны, ∟A — любой угол ромба.
Рассчитать объем песка для разных строительных целей
Нужный объем песка постоянно рассчитывают строители при выполнении широкого спектра работ:
засыпки и поднятия участков;
строительстве фундаментов и заборов;
формировании стяжки;
заливке отмостки;
приготовлении бетона;
благоустройстве территорий.
Точный расчет необходимого объема песка экономит время и деньги
В большинстве случаев для строительных целей используют карьерный или речной песок. Удельный вес 1 м³ карьерного песка – 1 500 кг, речного – 1 630 кг.
Речной песок более тяжелый, что объясняется меньшим размером зерен и большей плотностью материала. Приобретать песок рекомендуется в сухую погоду, когда в нем содержится минимум избыточной влаги.
Расчет объема песка для засыпки
Предположим, нам нужно засыпать участок площадью 6 соток (600 м²), подняв его на уровень 0,5 м.
Для определения объема песка следует умножить площадь участка на высоту засыпки. В нашем расчете – 600 х 0,5 = 300 м³.
После засыпки песок уляжется, на это нужно сделать поправку. Коэффициент уплотнения колеблется в пределах 1,05–1,3, в зависимости от вида песка. Для нашего примера возьмем среднюю величину 1,1, то есть добавим к рассчитанному объему еще 10 %. В результате получим 300 х 1,1 = 330 м³ песка.
Песок доставляют на самосвалах с разным объемом кузова
Заказывая материал, нужно обязательно уточнить, каким транспортом его доставят. В кузов КамАза, к примеру, помещается 12 м³ песка, МАЗа – 6 м³, ЗИЛа – 3 м³. При загрузке с горкой объем может увеличиться до 1,5 раза.
Расчет объема песка для бетонной смеси
При расчете количества песка для строительной смеси при создании фундаментов или стяжки нужно учитывать марку цемента.
Из-за неправильного объема песка снизится качество бетона
Сначала вычисляют необходимый объем бетона по формуле, приведенной выше. Исходя из класса бетона определяют требуемое количество песка.
Рассчитать его можно двумя способами:
По долевому соотношению песка и цемента
Для разных марок цемента используют разные пропорции. Показатель включения песка варьируется от 2–4,5 : 1.
Предположим, мы используем цемент марки М-200, для которого принято соотношение 2,8 : 1. Значит, на 100 кг цемента нужно взять 280 кг песка.
По процентному содержанию в бетоне
Зная необходимый объем бетона, просчитываем объем песка, исходя из его процентного содержания в смеси. В зависимости от класса бетона доля песка колеблется в пределах 29–36 %. Значит, нам потребуется минимум 29 м³ песка.
Расчет объема песка в конусной насыпи
Представим ситуацию, когда песок уже выгружен из самосвала и точно неизвестно, сколько его было в каждой машине. Просчитать объем конусной насыпи простым сложением не получится.
Для расчета объема песка в конусной насыпи нужно замерить ее радиус и высоту
Узнать точный объем песка в конусной насыпи можно по формуле: V = ⅓π х R² х H, где R – радиус конуса, H – его высота, π = 3,14.
Предположим, высота насыпи 1 метр, а радиус – 1,5 м. Рассчитываем:
Конечно, песок не дает идеального конуса, но примерно оценить объем таким образом возможно. А зная точный объем необходимого и имеющегося в наличии песка, проще планировать расход и поставки. Не будет простоев в работе, жесткой экономии, вынужденного снижения качества бетона и, соответственно, прочности готовых конструкций.
Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Объем правильного цилиндра через радиус и высоту цилиндра
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)

r — радиус основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Упрощение формулы:
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
S — площадь основания цилиндра
h — высота цилиндра

… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

d — диаметр основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Теория

Цилиндр может быть правильным или наклонным.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура.
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса.

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм³, см³, мл³.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько места для упаковки у вас есть при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание к единицам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см ³, м ³ и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см. ³.1 литр = 1000 мл = 1000 см ³.
Британская / английская система
В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Дополнительную информацию см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем прямоугольных тел

В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются. Вы можете умножать в любом порядке, так как это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см ³
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем — это только пропорция от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × ¹/₃
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr ² = 3,14 × 5 × 5 = 78,5 см ².
78,5 × 10 = 785
785 × 1/3 = 261,6667 см ³
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус ³.
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы вычислить радиус по окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала определите площадь одного из круглых концов цилиндра.
Площадь круга равна πr ² (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см ²
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см ² x 20 см = 392,70 см ³

Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы 4/3 × π × радиус ³.
Таким образом, объем сферы составляет:
.
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см ³
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см ²
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см ³
Таким образом, сфера больше по объему, чем пирамида.

Расчет объема твердых тел неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы 4/3 × π × радиус ³. В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.
0,5 × 4/3 × π × 203 = 16,755,16 см ³
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы πr ².
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см ³
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см ³.
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см ³). Однако вполне правильно выразить его как cm ³, поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.

Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Площадь треугольника (традиционный метод) с помощью калькулятора
Площадь треугольника (традиционный метод) с помощью калькулятора — Math Open Reference Количество квадратных единиц, необходимое для того, чтобы точно заполнить интерьер треугольник.Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить форму треугольника. Показанная формула пересчитает площадь с использованием этого метода.
Самый распространенный метод
Площадь треугольника, обычно называемая «половина основания, умноженная на высоту», определяется по формуле, приведенной ниже. где b — длина база
a — длина соответствующего высота
Вы можете выбрать любую сторону, чтобы быть база. Это не обязательно должен быть тот, который нарисован внизу треугольника.Высота должен быть тот, который соответствует выбранной вами базе. Высота — это линия, перпендикулярная выбранному основанию от противоположной вершины.
На рисунке выше одна сторона была выбрана в качестве основания и показана соответствующая высота.
Калькулятор
Используйте калькулятор выше, чтобы вычислить площадь треугольника.
Введите любые два значения, и другое будет вычислено. Например: введите базу и высоту и нажмите «Рассчитать».Площадь будет рассчитана.
Точно так же, если вы войдете в область и базу, будет рассчитана высота, необходимая для получения этой области.
Методы определения площади треугольника
Что попробовать
На рисунке выше нажмите «Высота замораживания». Когда вы теперь перетаскиваете точку A, обратите внимание, что область не меняется. Площадь зависит от основания и высоты, и ни один из них не меняется, когда вы перемещаете верхнюю вершину из стороны в сторону. Следовательно, все треугольники, которые вы можете создать таким образом, имеют одинаковую площадь.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Соответствие и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Объем призмы
А призма многогранник с двумя параллельными конгруэнтными гранями, называемыми основаниями, которые полигоны .
В объем из 3 -размерное твердое тело — это объем занимаемого пространства. Объем измеряется в кубических единицах ( в 3 , футов 3 , см 3 , м 3 и так далее). Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.
Громкость V призмы — это площадь основания B раз больше высоты час .
V знак равно B час
Примечание: Кубический сантиметр ( см 3 ) — куб, ребра которого измеряют 1 сантиметр.
Пример:
Найдите объем показанной призмы.
Решение
Формула объема призмы: V знак равно B час , где B это базовая площадь и час это высота.
Основание призмы — прямоугольник. Длина прямоугольника 9 см и ширина 7 см.
Площадь А прямоугольника длиной л и ширина ш является А знак равно л ш .
Итак, базовая площадь равна 9 × 7 или же 63 см 2 .
Высота призмы 13 см.
Заменять 63 для B а также 13 для час в V знак равно B час .
V знак равно ( 63 ) ( 13 )
Умножить.
V знак равно 819
Следовательно, объем призмы равен 819 кубические сантиметры.
Обнаружение формул площади — элементарная математика
Формулы площади
Учащиеся, неформально относящиеся к области как к «количеству двумерного« материала », содержащегося внутри области, могут придумать для себя большинство формул, которые их часто просят просто запомнить.Каждая формула, которую они изобретают заново, помогает им лучше понять (и запомнить) другие известные им формулы. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади.Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника. Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы его ни выбрали.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить всех чисел, мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длины этих сторон, измеренные в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый).Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась.Фактически, перпендикулярный разрез можно делать в любом месте по основанию.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина , что он должен быть тем, чем он является. Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким.Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если в результате не всегда получается идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма. В старших классах школьники смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основания?

Мы можем выбрать любую сторону в качестве базы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным. Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от его длины и тонкости, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник.Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея рассечения в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном случае.)
Заключите параллелограмм в прямоугольник.
Две части прямоугольника, которые находятся на , а не на внутри параллелограмма, являются конгруэнтными треугольниками.
Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник.Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же. Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят , как будто они соединяются вместе, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
При построении других формул площади (см. Ниже) мы захотим, чтобы использовал как наш способ определения площади параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы, , можем быть уверены, что перестановка частей не изменит область: это, в конце концов, то, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем, что это , иначе мы не можем полагаться на сделанные нами измерения.И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают. Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассечение треугольника
Мы можем разрезать треугольник на две части — одну из них треугольник, а другую — трапецию, разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с тем же основанием , но половиной высоты .
Итак, основание × полувысота дает площадь треугольника. Аналогичный разрез показывает полубаз × высота .Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади вдвое
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.
Площадь параллелограмма равна основанию × высоте , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади вдвое
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание равно сумме двух оснований трапеции.Таким образом, площадь параллелограмма составляет по высоте × ( base1 + base2 ). Но эта площадь составляет две трапеции, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.
В случае трапеции основания не могут быть выбраны произвольно. Две параллельные стороны являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь составляет полувысоты × ( base1 + base2 ). Поскольку параллелограмм состоит из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × высота × ( base1 + base2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части в форме параллелограмма. Это можно сделать несколькими способами:
Разрежьте более короткую диагональ (а), чтобы получились два равных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.
После разрезания ромба на два равных треугольника мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь кайта
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с более длинной диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты. Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
Определение объема и площади поверхности прямоугольных твердых тел
Результаты обучения
Найдите объем и площадь поверхности прямоугольного твердого тела
Тренер по черлидингу приказывает команде красить деревянные ящики в школьные цвета, чтобы на них стоять на играх.(См. Изображение ниже). Количество краски, необходимое для покрытия внешней стороны каждой коробки, — это площадь поверхности, квадратная мера общей площади всех сторон. Количество места внутри обрешетки — это объем, кубическая мера.
Деревянный ящик имеет форму прямоугольного твердого тела.

Каждый ящик имеет твердую прямоугольную форму. Его размеры — длина, ширина и высота. Прямоугольное тело, показанное на изображении ниже, имеет длину [латекс] 4 [/ латекс] единиц, ширину [латекс] 2 [/ латекс] единиц и высоту [латекс] 3 [/ латекс] единиц.Вы можете сказать, сколько всего кубических единиц? Давайте посмотрим слой за слоем.
Разделение прямоугольного твердого тела на слои упрощает визуализацию количества кубических единиц, которые оно содержит. Этот прямоугольный массив [латекс] 4 [/ латекс] на [латекс] 2 [/ латекс] на [латекс] 3 [/ латекс] имеет [латекс] 24 [/ латекс] кубических единиц.

Всего [латекс] 24 [/ латекс] куб. Обратите внимание, что [latex] 24 [/ latex] — это [latex] \ text {length} \ times \ text {width} \ times \ text {height} \ text {.} [/ Latex]

Объем [латекс] V [/ латекс] любого прямоугольного твердого тела является произведением длины, ширины и высоты.
[латекс] V = LWH [/ latex]
Мы могли бы также написать формулу для объема прямоугольного твердого тела через площадь основания. Площадь основы [латекс] B [/ latex] равна [латексу] \ text {length} \ times \ text {width} \ text {.} [/ Latex]
[латекс] B = L \ cdot W [/ latex]
Мы можем заменить [latex] B [/ latex] на [latex] L \ cdot W [/ latex] в формуле объема, чтобы получить другую форму формулы объема .

Теперь у нас есть другая версия формулы объема для прямоугольных тел.Давайте посмотрим, как это работает с прямоугольным телом [латекс] 4 \ times 2 \ times 3 [/ latex], с которого мы начали. См. Изображение ниже.

Чтобы найти площадь поверхности прямоугольного твердого тела, подумайте о том, чтобы найти площадь каждой из его граней. Сколько граней у прямоугольного тела наверху? Вы можете увидеть три из них.
[латекс] \ begin {array} {ccccccc} {A} _ {\ text {front}} = L \ times W \ hfill & & & {A} _ {\ text {side}} = L \ times W \ hfill & & & {A} _ {\ text {top}} = L \ times W \ hfill \\ {A} _ {\ text {front}} = 4 \ cdot 3 \ hfill & & & {A} _ { \ text {side}} = 2 \ cdot 3 \ hfill & & & {A} _ {\ text {top}} = 4 \ cdot 2 \ hfill \\ {A} _ {\ text {front}} = 12 \ hfill & & & {A} _ {\ text {side}} = 6 \ hfill & & & {A} _ {\ text {top}} = 8 \ hfill \ end {array} [/ latex]
Уведомление для каждого из трех лиц, которые вы видите, есть идентичное противоположное лицо, которое не отображается.
[латекс] \ begin {array} {l} S = \ left (\ text {front} + \ text {back} \ right) \ text {+} \ left (\ text {left side} + \ text {right side} \ right) + \ left (\ text {top} + \ text {bottom} \ right) \\ S = \ left (2 \ cdot \ text {front} \ right) + \ left (\ text {2} \ cdot \ text {left side} \ right) + \ left (\ text {2} \ cdot \ text {top} \ right) \\ S = 2 \ cdot 12 + 2 \ cdot 6 + 2 \ cdot 8 \\ S = 24 + 12 + 16 \\ S = 52 \ text {sq. units} \ end {array} [/ latex]
Площадь поверхности [latex] S [/ latex] прямоугольного твердого тела, показанного выше, составляет [латекс] 52 [/ latex] квадратных единиц.
В общем, чтобы найти площадь поверхности прямоугольного твердого тела, помните, что каждая грань представляет собой прямоугольник, поэтому его площадь является произведением его длины и ширины (см. Изображение ниже).Найдите площадь каждого лица, которое вы видите, а затем умножьте каждую площадь на два, чтобы учесть лицо на противоположной стороне.
[латекс] S = 2LH + 2LW + 2WH [/ латекс]
Для каждой обращенной к вам грани прямоугольного твердого тела есть еще одна грань на противоположной стороне. Всего [латексных] лиц 6 [/ латексных].
Объем и площадь прямоугольного твердого тела
Для прямоугольного твердого тела длиной [латекс] L [/ латекс], шириной [латекс] W [/ латекс] и высотой [латекс] H: [/ латекс]
Выполнение задания по манипуляции математикой «Раскрашенный куб» поможет вам лучше понять объем и площадь поверхности.
, пример
Для прямоугольного твердого тела длиной [латекс] 14 [/ латекс] см, высотой [латекс] 17 [/ латекс] см и шириной [латекс] 9 [/ латекс] см найдите 1. объем и 2. площадь поверхности. .
Решение
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз.
Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и
пометьте его данной информацией.
1.
Шаг 2. Определите , что вы ищете. объем прямоугольный сплошной
Шаг 3. Имя. Выберите переменную для ее представления. Пусть [латекс] V [/ латекс] = объем
Шаг 4. Translate.
Напишите соответствующую формулу.
Запасной.
[латекс] V = LWH [/ латекс]
[латекс] V = \ mathrm {14} \ cdot 9 \ cdot 17 [/ латекс]
Шаг 5. Решите уравнение. [латекс] V = 2,142 [/ латекс]
Шаг 6. Чек
Мы предоставляем вам проверить ваши расчеты.
Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] \ text {1,034} [/ латекс] квадратных сантиметров.
2.
Шаг 2. Определите , что вы ищете. площадь поверхности твердого тела
Шаг 3. Имя. Выберите переменную для ее представления. Пусть [латекс] S [/ латекс] = площадь поверхности
Шаг 4. Translate.
Напишите соответствующую формулу.
Запасной.
[латекс] S = 2LH + 2LW + 2WH [/ латекс]
[латекс] S = 2 \ left (14 \ cdot 17 \ right) +2 \ left (14 \ cdot 9 \ right) +2 \ left (9 \ cdot 17 \ right) [/ latex]
Шаг 5. Решите уравнение. [латекс] S = 1,034 [/ латекс]
Шаг 6. Проверка: Перепроверьте с помощью калькулятора.
Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] 1034 [/ латекс] квадратных сантиметров.
, пример
Прямоугольный ящик имеет длину [латекс] 30 [/ латекс] дюймов, ширину [латекс] 25 [/ латекс] дюймов и высоту [латекс] 20 [/ латекс] дюймов.Найдите его 1. объем и 2. площадь поверхности.
Показать решение
Решение
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз.
Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и
пометьте его данной информацией.
1.
Шаг 2. Определите , что вы ищете. объем ящика
Шаг 3. Имя. Выберите переменную для ее представления. let [latex] V [/ latex] = объем
Шаг 4. Translate.
Напишите соответствующую формулу.
Запасной.
[латекс] V = LWH [/ латекс]
[латекс] V = 30 \ cdot 25 \ cdot 20 [/ латекс]
Шаг 5. Решите уравнение. [латекс] V = 15 000 [/ латекс]
Шаг 6. Проверка: Еще раз проверьте свои математические расчеты.
Шаг 7. Ответьте на вопрос. Объем [латекс] 15 000 [/ латекс] кубических дюймов.
2.
Шаг 2. Определите , что вы ищете. Площадь ящика
Шаг 3. Имя. Выберите переменную для ее представления. let [латекс] S [/ latex] = площадь поверхности
Шаг 4. Перевести.
Напишите соответствующую формулу.
Запасной.
[латекс] S = 2LH + 2LW + 2WH [/ латекс]
[латекс] S = 2 \ left (30 \ cdot 20 \ right) +2 \ left (30 \ cdot 25 \ right) +2 \ left (25 \ cdot 20 \ right) [/ latex]
Шаг 5. Решите уравнение. [латекс] S = 3,700 [/ латекс]
Шаг 6. Проверка: Убедитесь сами!
Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] 3700 [/ латекс] квадратных дюймов.
Калькулятор площади
| Определение
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел. Если вы когда-нибудь задумывались, как найти площадь поверхности или площадь боковой поверхности, этот калькулятор поможет вам. В этой статье вы можете найти формулы для площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной / треугольной призмы.Мы также объясним, как вычислить площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности — общая площадь, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности может быть разделена на сумму базовых площадей и площади боковой поверхности . Боковая поверхность — это площадь всех сторон объекта, за исключением его основания и вершины.Это разделение используется для форм, где существует очевидное различие между основанием и другой частью — например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основы (например, в кубе или коробке), и мы не используем его для гладких поверхностей, таких как сфера.
Формула площади поверхности …
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел. Формула зависит от типа твердого тела.
Площадь поверхности сферы: A = 4πr² , где r обозначает радиус сферы.
Площадь поверхности куба: A = 6a² , где a — длина стороны.
Площадь поверхности цилиндра: A = 2πr² + 2πrh , где r — радиус, а h — высота цилиндра.
Площадь поверхности конуса: A = πr² + πr√ (r² + h²) , где r — радиус, а h — высота конуса.
Площадь поверхности прямоугольной призмы (прямоугольник): A = 2 (ab + bc + ac) , где a , b и c — длины трех сторон кубоида.
Площадь поверхности треугольной призмы: A = 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) + h * (a + b + c) , где a , b и c — это длины трех сторон основания треугольной призмы, а h — высота (длина) призмы.
Площадь поверхности пирамиды: A = l * √ (l² + 4 * h²) + l² , где l — длина стороны квадратного основания, а h — высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы рассчитать площадь поверхности сферы, все, что вам нужно знать, — это радиус сферы или ее диаметр.
A = 4 * π * r² , где r — радиус.
Поскольку мы знаем, что диаметр сферы равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
A = 4 * π * (d / 2) ² = π * d² , где d — диаметр сферы.
Для вывода этой формулы площади поверхности требуется интегрирование. Если вам интересно, посмотрите это доказательство.
Площадь цилиндра
Чтобы узнать площадь поверхности цилиндра, у вас должно быть два значения: радиус (или диаметр) основания и высота цилиндра.Общее уравнение обычное — площадь основания умножить на высоту . В нашем случае круг — это основа.
Откуда взялась эта формула? Вы можете записать уравнение для площади поверхности цилиндра как:
A = A (сбоку) + 2 * A (основание)
Найти площадь основания несложно — запомним известную формулу площади круга: A (основание) = π * r² . Но какова форма боковой поверхности? Попробуйте представить, что мы его «разворачиваем».Вы узнаете это? Это прямоугольник ! Длина одной стороны равна высоте цилиндра, а вторая — окружности развернутого круга.
A (база) = π * r²
A (сбоку) = h * (2 * π * r)
Площадь конуса
Мы можем разделить поверхность конуса на две части:
A = A (боковой) + A (основание) , так как у нас только одно основание, в отличие от цилиндра.
Основание — это снова площадь круга A (основание) = π * r² , но происхождение площади боковой поверхности может быть не так очевидно:
A (боковой) = π * r * √ (r² + h²)
Давайте посмотрим на этот вывод по шагам:
Раскатайте боковую поверхность. Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса).
Для окружности с радиусом s, , длина окружности равна 2 * π * s . Длина дуги сектора равна 2 * π * r .
Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
A (сбоку) = (s * (длина дуги)) / 2 = (s * 2 * π * r) / 2 = π * r * s
Формула может быть получена из пропорции: отношение площадей фигур такое же, как отношение длины дуги к окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (окружность большого круга) так:
(площадь сектора) / (π * s²) = (2 * π * r) / (2 * π * s)
(площадь сектора) = (π * s²) * (2 * π * r) / (2 * π * s)
Обычно нам задают не s , а h , что составляет высоты конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Таким образом, формула площади боковой поверхности выглядит следующим образом:
A (боковой) = π * r * √ (r² + h²)
Наконец, сложите площади основания и боковой части, чтобы найти окончательную формулу для площади поверхности конуса :
A = A (сбоку) + A (основание) = π * r * s + π * r² для r и s или
A = π * r * √ (r² + h²) + π * r² для r и h .
Площадь куба
Площадь поверхности куба — это самое простое, что вы можете себе представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
.
Поскольку площадь квадрата является произведением длины его сторон, окончательная формула для определения площади поверхности куба будет:
A = 6 * l² , где l — сторона квадрата
Площадь пирамиды
Пирамида — это трехмерное тело с многоугольным основанием и треугольными боковыми гранями.Когда вы слышите пирамида , обычно предполагается, что это правильная квадратная пирамида . Обычный означает, что он имеет правильное основание многоугольника и является правой пирамидой (вершина прямо над центром тяжести его основания) и квадратом — что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
A = l * √ (l² + 4 * h²) + l² , где l — сторона основания, а h — высота пирамиды
Опять же, мы можем разделить уравнение на:
A = A (основание) + A (сбоку) = A (основание) + 4 * A (боковая поверхность)
Основание имеет форму квадрата, поэтому A (основание) = l² .Чтобы рассчитать площадь боковой поверхности, начнем с площади одной треугольной грани:
Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
Вычислите гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
c = √ (h² + (l / 2) ²) = √ (h² + l² / 4)
Площадь треугольника (в нашем случае это равнобедренный треугольник) можно рассчитать как:
A = высота * основание / 2 так
A (боковая сторона) = √ (h² + l² / 4) * l / 2
Итак, окончательная формула площади поверхности пирамиды:
A = l² + 4 * √ (h² + l² / 4) * l / 2 = l² + 2 * l * √ (h² + l² / 4)
A = l² + l * √ (4 * h² + l²)
Площадь прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, все, что вам нужно сделать, это вычислить площади сторон прямоугольника:
где:
A1 = длина * ширина
A2 = ш * в
A3 = длина * высота
Таким образом, окончательная формула:
A = 2 * (д * ш + ш * в + д * в)
Площадь поверхности треугольной призмы
Чтобы понять, откуда взялась формула для площади поверхности треугольной призмы, давайте взглянем на этот вывод:
В этом случае легко вычислить площадь боковой поверхности.Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
A (сбоку) = a * h + b * h + c * h = h * (a + b + c)
, который мы также можем записать сокращенно:
A (сбоку) = h * P , где P — периметр базового треугольника
Затем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дают. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A (основание) = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)))
Окончательная формула площади поверхности треугольной призмы:
A = A (сбоку) + 2 * A (основание)
A = h * (a + b + c) + 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c ))
Площадь поверхности тела
Вы можете рассчитать поверхность любого твердого тела, например, вашего тела — это не обязательно должна быть простая геометрическая форма! Если вам интересно, какова площадь внешней поверхности человеческого тела, воспользуйтесь этим калькулятором площади поверхности тела.
Как рассчитать площадь поверхности шара?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие шаги:
Определите радиус сферы. Можно принять радиус 10 см.
Введите это значение в формулу A = 4πr² .
Рассчитайте результат: A = 4π * 10² = 1256 см² .
Вы также можете использовать этот калькулятор площади поверхности, чтобы найти радиус сферы, если вы знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить это в см², дюймах, фут², м², а также в акрах и гектарах.
Если вы хотите определить объем любого из этих твердых веществ, воспользуйтесь нашим калькулятором объема.
Площадь треугольника равна основанию, умноженному на высоту, деленную на 3 | Сунил Сингх
Несколько недель назад я спросил своего сына, который учится в 7-м классе, что ты делаешь по математике? Он ответил тоном несомненной ровности, «площадь треугольника».Прежде всего, позвольте мне сказать, что учитель моего сына просто потрясающий — много сочувствия и даже вплетает идеи Fortnite в свой класс. Однако я знал, куда пойдет этот урок по треугольной области, — и не пошел.
Как и тысячам студентов, моему сыну дали формулу треугольника, а затем он провел два дня, занимаясь рабочими листами, вставляя то, что не должно было быть инертной передачей информации. Как только площадь треугольника определена, урок окончен. Больше ничего не остается делать, кроме некоторых задач по сухой алгебре, в которых ученики должны вместо этого найти высоту или основание.
Большая часть математики до сих пор начинается так во многих классах по всему миру — с знаков препинания. Именно здесь идея прямого обучения ощущается как телефон с дисковым набором номера в мире математического образования.
Урок окончен. Урок должен был начаться примерно так…
Всю статью за 2014 год можно найти здесь. Простое математическое соотношение, но с двумя совершенно разными результатами. Один — это шаблонный, сухой и узкий экскурс в кошмар рабочих листов.Другой — это естественная, историческая и игривая возня с тем, чем на самом деле является математика, — суетливое, открытое творчество.
Наше представление математических соотношений / формул настолько бесплодно, что мы можем легко изменить константы, и на результат не будет никакого влияния, кроме другого ответа. Я имею в виду, что, если мы выучили площадь треугольника по неправильной формуле? Сколько времени потребуется, чтобы студент вернулся к нам и сказал, что это неправильно? Мне страшно думать о предположении, что никто не станет оспаривать эту идею, и даже если они это сделают, не с математической точки зрения — просто из-за неверной информации.
В праздничные дни я планирую познакомить своих детей с теоремой Пифагора — но самым окольным, «чудаковатым» способом! Географическая доска — прекрасный ресурс для детей, чтобы играть с фигурами. И, как вы можете видеть на картинке выше, даже цифровые модели кажутся игривыми и реальными.
Я попрошу своих детей построить на Географической доске как можно больше квадратов разного размера. Это тот ответ, которого я отчасти жду.
Эти ответы можно проверить визуально и подкрепить фактическими ответами 1, 4, 9, 16.Выполнение этого действия на Geoboard также автоматически создает «обратные L» — последовательные нечетные числа, которые добавляются для получения больших квадратов. Это приятное дополнительное преимущество!
Конечно, я естественно спрошу их, есть ли еще квадраты разного размера. Вероятно, будет какое-то жужжание и бормотание, какие-то проб и ошибок, возможно, даже будут созданы дубликаты, но я не ожидаю квадрата другого размера — хотя все может случиться!
Следующее, что я им покажу, это:
Я надеюсь на какой-то толчок здесь! «Это не квадрат» или, может быть, «Это такой же размер, как… ммм….один из других »…
Я надеюсь, что мой сын помнит теорему Пика, которую я показал ему два года назад. Я упомяну, что мы можем проверить, действительно ли этот квадрат имеет другой размер (другую площадь), с помощью теоремы Пика:
Я обычно использую букву «е» для внешних точек. Итак, используя Пик для нашего многоугольника, который оказывается квадратным, мы получаем A = 1 + 4/2, вычитаем 1 = 2.
Площадь этого квадрата равна 2!
Теперь я спрошу своих детей, если площадь квадрата равна 2, какова сторона квадрата? Какое число, умноженное само на себя, дает… 2? Пока они это пережевывают, я построю это.
Игра началась!
Два желтых квадрата имеют площадь 1. Большой квадрат равен двум. Хммм… 🙂
Теперь это мой портал в Теорему Пифагора. Формула записывается на доске за несколько секунд. Выполнение нескольких примеров займет несколько минут. Затем студентов просят сделать еще 50. В то время могла быть соткана такая история.
Пока математика больше не будет порабощена тестами и производительностью на этих тестах, будет мало времени для математических прогулок нравится это.
К счастью, все больше и больше преподавателей математики меняют то, как их ученики пересекаются и изучают математику. Да, тесты еще нужны.
No related posts.