Площадь длина на ширину: «Как найти площадь прямоугольника?» – Яндекс.Кью
Обозначение: высота, ширина, длина. Ширина
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка.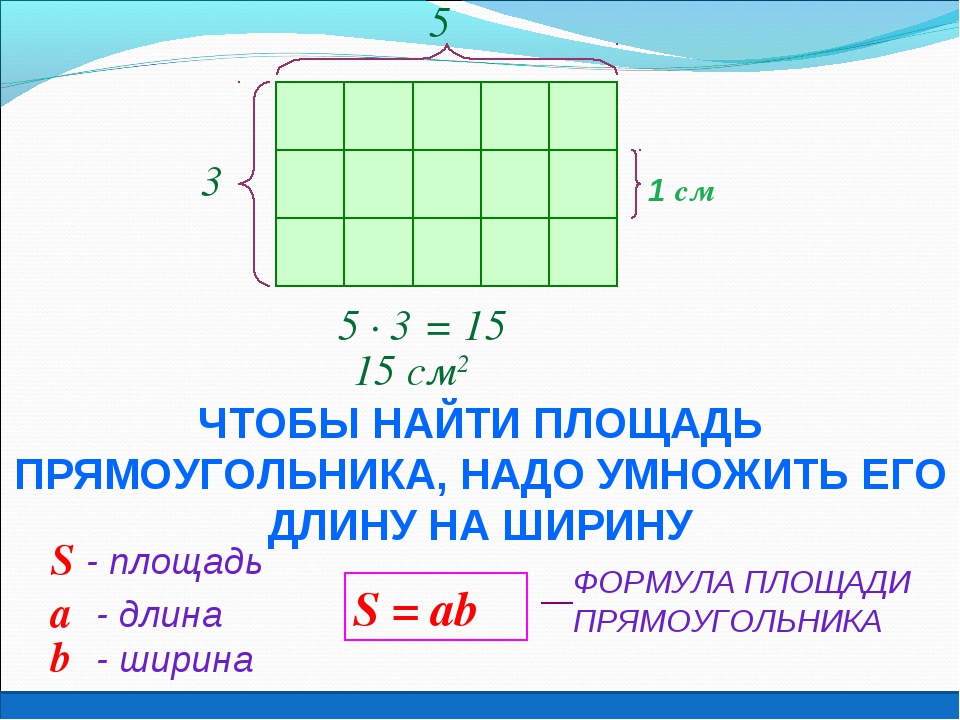 Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.
Урок 22. площадь прямоугольника — Математика — 3 класс
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
Правильный ответ:
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ:32см2.
Математика для блондинок: Как найти площадь прямоугольника?
Вот такая вот задача про площадь прямоугольника из учебника по алгебре за 7 класс:Если ширину прямоугольника увеличить на 2 дм, а длину уменьшить на 0,5 м, то получим квадрат, площадь которого на 50 дм² меньше, чем площадь прямоугольника. Найдите площадь прямоугольника.
Интересно, в 7 классе изучают системы линейных уравнений с двумя неизвестными? Судя по тому, что задача из учебника по алгебре, именно так нужно решать эту задачу. Тупо составляем систему уравнений, тупо решаем — тоска смертная. Если я здесь просто напишу решение, а вы его просто спишите, то умнее вы от этого не станете. Предлагаю решить эту задачу, а систему уравнений с решением мы в конце состряпаем.
Тупо составляем систему уравнений, тупо решаем — тоска смертная. Если я здесь просто напишу решение, а вы его просто спишите, то умнее вы от этого не станете. Предлагаю решить эту задачу, а систему уравнений с решением мы в конце состряпаем.
Что такое квадрат? Это такой прямоугольник, у которого стороны равны. Что такое прямоугольник? Это квадрат, у которого стороны разные. Своим преподавателям математики это говорить не советую — для них это прозвучит как осквернение святынь. Лично я подобными «определениями» пользуюсь постоянно, очень даже помогает. Ведь математические свойства геометрических объектов они передают очень точно.
Для решения задачи, обозначим стороны прямоугольника: a — это длина, b — это ширина. Теперь начинаем заново читать условие задачи.
«Если ширину прямоугольника увеличить на 2 дм…». На языке математики это можно записать так: b+2.
«… а длину уменьшить на 0,5 м…» Вот здесь прошу обратить особое внимание — только абсолютно безграмотные люди в
одной задаче используют разные единицы измерения длины.
«… то получим квадрат…» Ну, с квадратом мы уже разобрались — у него стороны равны. Вот этот геометрический феномен мы запишем математическими иероглифами:
a-5=b+2
Что это нам дает? Пожонглировав этим выражением, мы можем длину одной стороны выразить через длину другой стороны. В будущем это нам пригодится. Лично мне не нравится знак «минус». Сейчас мы от него избавимся.
a-5=b+2
a=b+2+5
a=b+7
Что-то мы отвлеклись от условия задачи. Включаем обратную перемотку и читаем фразу целиком: «… то получим квадрат, площадь которого на 50 дм² меньше, чем площадь прямоугольника».
| Как найти площадь прямоугольника |
a*b-(a-5)*(b+2)=50
a*b-(a*b-5b+2a-10)=50
a*b-a*b+5b-2a+10=50
5b-2a+10=50
5b-2a=50-10
5b-2a=40
Что дальше? А вот теперь мы можем вместо стороны а подставить результат первоначального жонглирования
5b-2a=40
5b-2(b+7)=40
5b-2b-14=40
3b=40+14
3b=54
b=18
Ширину прямоугольника мы уже знаем — 18 дециметров. Ищем длину.
a=b+7
а=18+7
а=25
Теперь мы без труда можем определить площадь прямоугольника: 25*18=450 дм². В тетрадке можно записать всё это как систему двух уравнений с двумя неизвестными. Я приведу сразу две системы уравнений, выбирайте любую.
В тетрадке можно записать всё это как систему двух уравнений с двумя неизвестными. Я приведу сразу две системы уравнений, выбирайте любую.
| Как найти площадь прямоугольника. Решение. |
Правило 1. Поле / КонсультантПлюс
Правило 1. ПолеОПРЕДЕЛЕНИЯ.
Поле — это общая площадь, показанная на плане. Поле состоит из следующих частей:
Игровое поле — это площадь (как показано на плане) между линями ворот и боковыми линиями. Эти линии не являются частью игрового поля.
Игровая площадь состоит из игрового и зачетного поля (как показано на плане).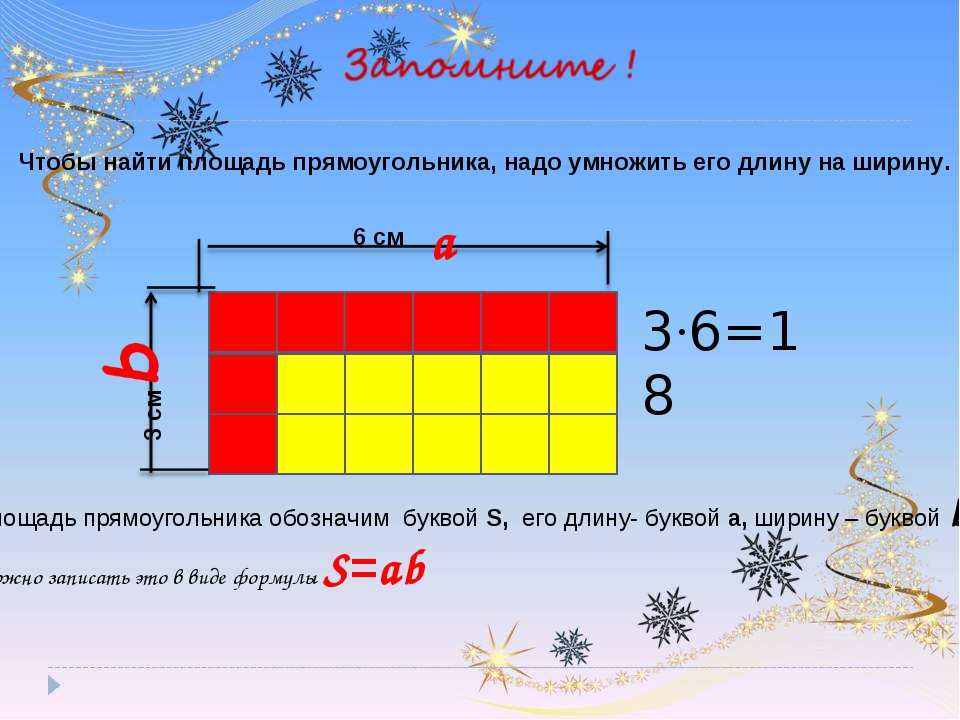 Боковые линии, боковые линии зачетного поля и линии «мертвого мяча» не являются частью игровой площади.
Боковые линии, боковые линии зачетного поля и линии «мертвого мяча» не являются частью игровой площади.
Игровое пространство состоит из игровой площади и окружающей ее территории в пределах 5 метров (если это практически выполнимо), которая называется площадью по периметру.
Зачетное поле является площадью между линией ворот, линией «мертвого мяча» и боковыми линиями зачетного поля. Оно включает линию ворот, но не включает линию «мертвого мяча» и боковые линии зачетного поля.
«Зона 22 м» — площадь между линией ворот и линией 22 м, включая линию 22 м, но исключая линию ворот.
План, включая все слова и цифры на нем, является частью настоящих правил игры.
1.1. ПОВЕРХНОСТЬ ИГРОВОГО ПРОСТРАНСТВА.
(a) Требование. Поверхность должна быть безопасной для игры в любое время.
(b) Тип покрытия. Поверхность должна быть покрыта травой или, возможно, песком, глиной, снегом или искусственной травой. Игра может проводиться на снегу, при условии, что снег и поверхность под ним являются безопасными для игры. Ни в коем случае поверхность не должна быть жесткой, т.е. покрытой бетоном или асфальтом. В случае использования покрытия искусственной травой, оно должно соответствовать Положению 22 World Rugby.
Ни в коем случае поверхность не должна быть жесткой, т.е. покрытой бетоном или асфальтом. В случае использования покрытия искусственной травой, оно должно соответствовать Положению 22 World Rugby.
1.2. НЕОБХОДИМЫЕ РАЗМЕРЫ ИГРОВОГО ПРОСТРАНСТВА.
(a) Размеры. Игровое поле не должно превышать 100 метров в длину. Каждое зачетное поле не должно превышать 22 метров в длину. Игровая площадь не должна превышать 70 метров в длину.
(b) Длина и ширина игровой площади должны быть максимально приближены к указанным размерам. Все площади должны быть прямоугольными.
(c) Расстояние от линии ворот до линии «мертвого мяча» не должно быть меньше, чем 10 метров, если это практически выполнимо.
(d) В случае:
(i) матчей между главной национальной командой или второй национальной командой, представляющей Союз, против старшей или второй национальной командой, представляющей другой Союз; и
(ii) международных матчей по регби-7, размеры должны быть как можно ближе к максимальным, а также игровое поле должно быть не меньше 94 метров в длину и 68 метров в ширину с минимальной длиной зачетного поля 6 метров. Союзы, которые желают изменить минимальные или максимальные размеры поля, должны обратиться в World Rugby для получения соответствующего разрешения.
Союзы, которые желают изменить минимальные или максимальные размеры поля, должны обратиться в World Rugby для получения соответствующего разрешения.
(e) Площадь по периметру игрового поля должна быть не меньше 5 метров в ширину, если это осуществимо.
1.3. РАЗМЕТКА ИГРОВОГО ПРОСТРАНСТВА.
(a) Сплошные линии.
Линии «мертвого мяча» и боковые линии зачетного поля, которые не являются частью зачетного поля.
Линии ворот, которые являются частью зачетного поля, но не игрового поля.
Линии 22 м, параллельные линии ворот.
Центральная линия, которая также параллельна линии ворот.
Боковые линии, которые не являются частью игрового поля.
(b) Пунктирные линии:
Все линии, кроме сплошных линий, являются пунктирными линиями, состоящими из штрихов длиной 5 метров.
Две пунктирные линии проходят параллельно центральной линии поля в 10 метрах от нее с каждой стороны. Они называются пунктирными линиями 10 метров. Пунктирные линии 10 метров пересекают пунктирные линии, проходящие параллельно боковым линиям в 5 метрах и 15 метрах от них.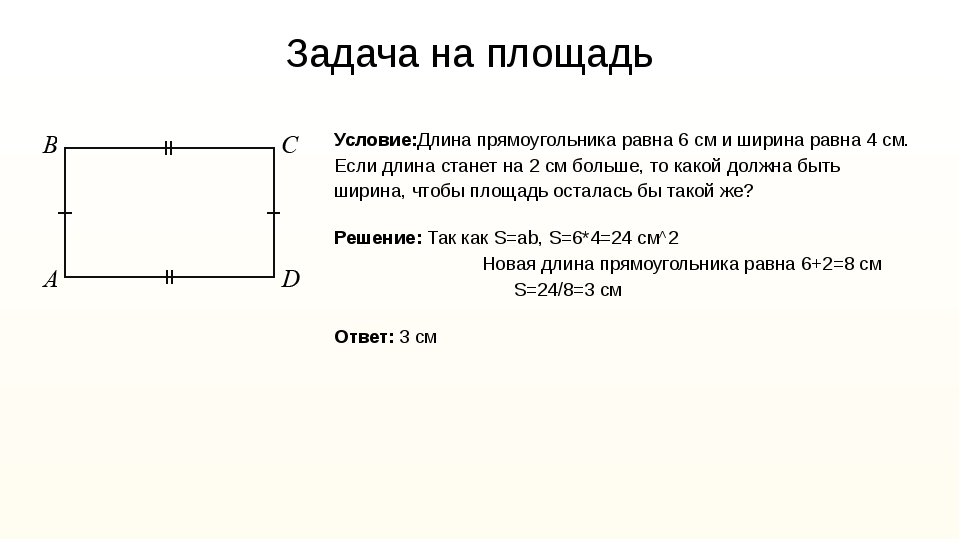
Две пунктирные линии проходят параллельно боковым линиям поля в 5 метрах от них. Они начинаются у пунктирных линий 5 метров, параллельных линиям ворот, и пересекают обе линии 22 метров, обе линии 10 метров и центральную линию поля. Они называются пунктирными линиями 5 метров.
Две пунктирные линии проходят параллельно боковым линиям поля на расстоянии 15 метров от них. Эти пунктирные линии начинаются у пунктирных линий 5 метров, параллельных линиям ворот, и пересекают обе линии 22 метров, обе пунктирные линии 10 метров и центральную линию поля. Они называются пунктирными линиями 15 метров.
Две линии их шести штрихов проходят параллельно линиям ворот в 5 метрах от них. Два штриха располагаются так, что их середины находятся в 5 метрах и 15 метрах от боковой линии с каждой стороны поля. Другие два штриха располагаются перед каждой линией ворот с промежутком в 5 метров между ними.
(c) Центр:
Одна линия длиной 0,5 метров делит центральную линию поля пополам.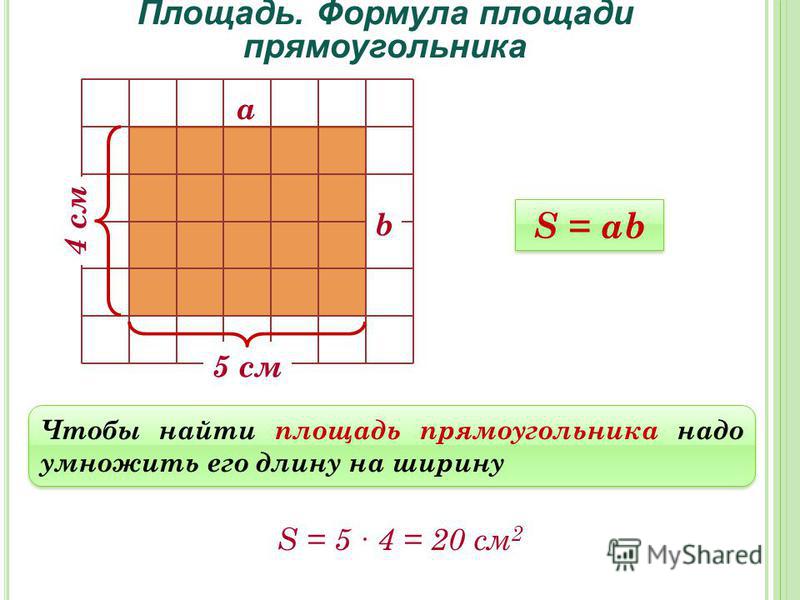
1.4. РАЗМЕРЫ СТОЕК ВОРОТ И ПЕРЕКЛАДИНЫ.
(a) Расстояние между стойками ворот — 5,6 метра.
(b) Перекладина расположена между стойками таким образом, чтобы ее верхний край находился на высоте 3 метра от земли.
(c) Минимальная высота стоек ворот — 3,4 метра.
(d) Если стойки ворот покрыты защитой, то расстояние между линией ворот и внешним краем защиты не должно превышать 300 мм.
1.5. ФЛАЖКИ.
(a) На поле установлено 14 флажков, каждый высотой минимум 1,2 метра над землей.
(b) Флажки должны быть установлены на пересечении боковых линий зачетного поля и линии ворот, а также боковых линий зачетного поля и линий «мертвого» мяча. Эти восемь флажков находятся вне зачетного поля и не являются частью игровой площади.
(c) Флажки должны быть установлены на одной линии с линиями 22 м и центральной линией, на расстоянии 2 метров с наружной стороны боковых линий и внутри игрового пространства.
1.6. ВОЗРАЖЕНИЯ ОТНОСИТЕЛЬНО ИГРОВОГО ПОЛЯ.
(a) Если любая из команд имеет возражения относительно поля или его разметки, она должна сообщить об этом судье до начала матча.
(b) Судья должен попытаться разрешить проблему, но не должен начинать матч, если любая часть поля считается опасной для игры.
Площадь прямоугольника способы. Как узнать площадь прямоугольника
Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Площадь квадрата и как ее найти
Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a
2
, где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Для этого необходимо извлечь квадрат из указанной величины.
Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.
Как найти периметр квадратаПериметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.
Пример:
- сторона квадрата = 5, следовательно, P = 4*5 = 20
- сторона квадрата = 3, следовательно, Р = 4*3 = 12
Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.
Например: как найти периметр квадрата, если известна площадь, равная 144?
Шаги решения:
- Выясняем длину одной стороны: а = √144 = 12
- Находим периметр: Р = 4*12 = 48.
Нахождение периметра вписанного квадрата
Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Алгоритм решения:
- так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
- затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
- делим уравнение на 2: (a 2 ) = 2(r) 2 ;
- извлекаем корень: a = √(2r).
В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).
- Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).
Задача:
Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a
2
) = 10
2
, то есть 2a
2
= 100. Делим полученное на два и в результате: a
2
= 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Рассмотрим еще один вопрос
Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?
Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см
2
, найдите его периметр.
Шаги решения:
- Находим сторону квадрата: а = √25 = 5.
- Находим сам периметр: Р = 4*а = 4*5 = 20.
Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр . На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2.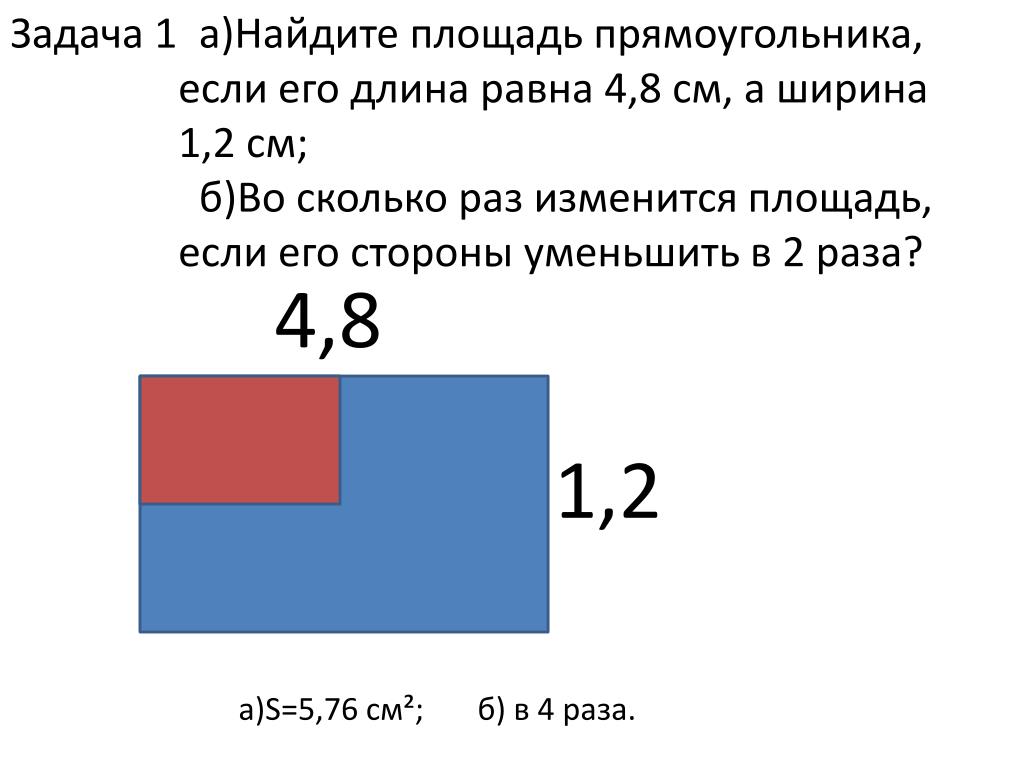 Значит, мы можем выполнить следующее действие:
Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения. При умножении каких чисел получается ответ 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Запишем решение.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо 12 уменьшить в 2 раза.
Ответ: площадь треугольника 6 см 2 .
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др.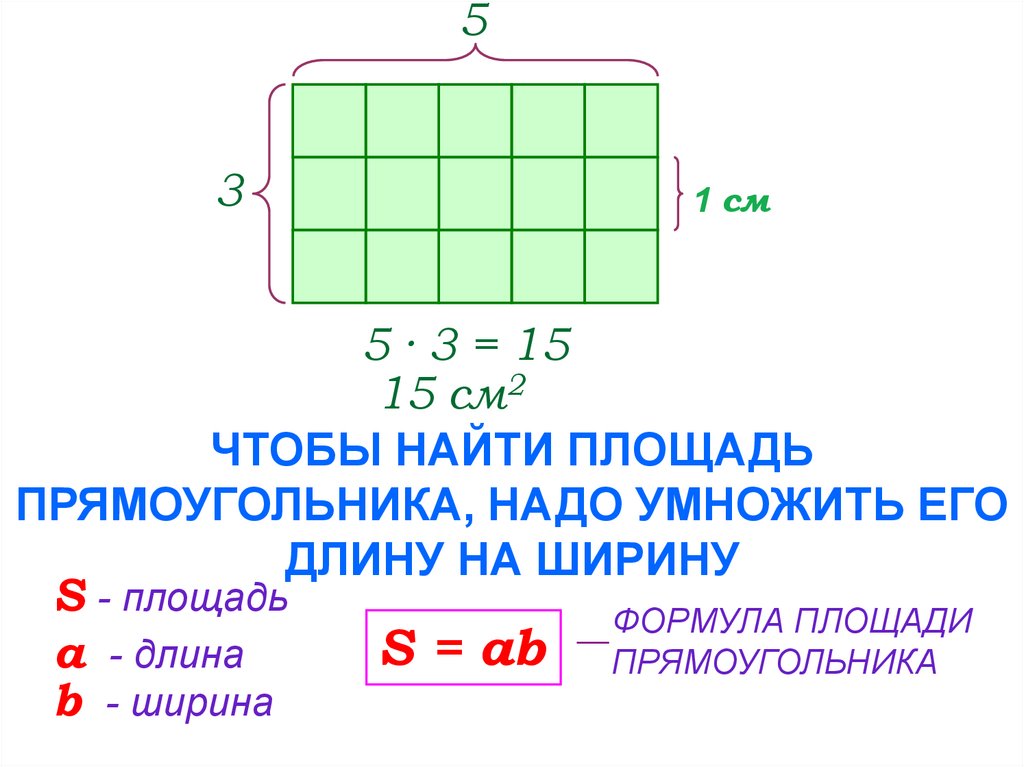 Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.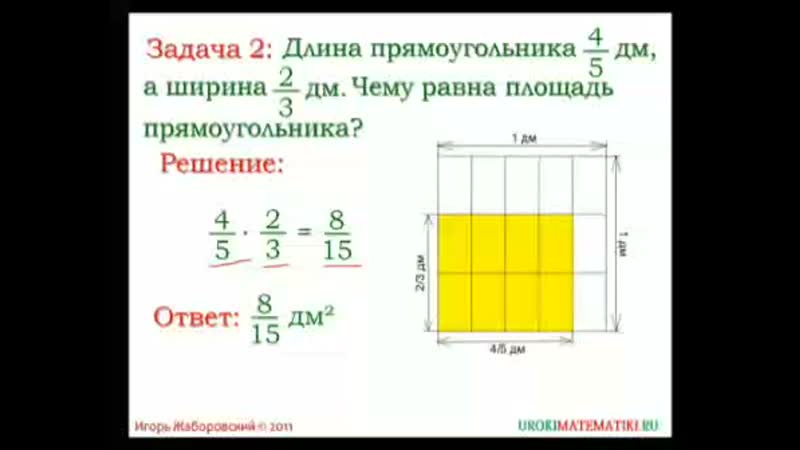
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата.
 Учитывая, что все стороны квадрата равны, получаем:
Учитывая, что все стороны квадрата равны, получаем:P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2.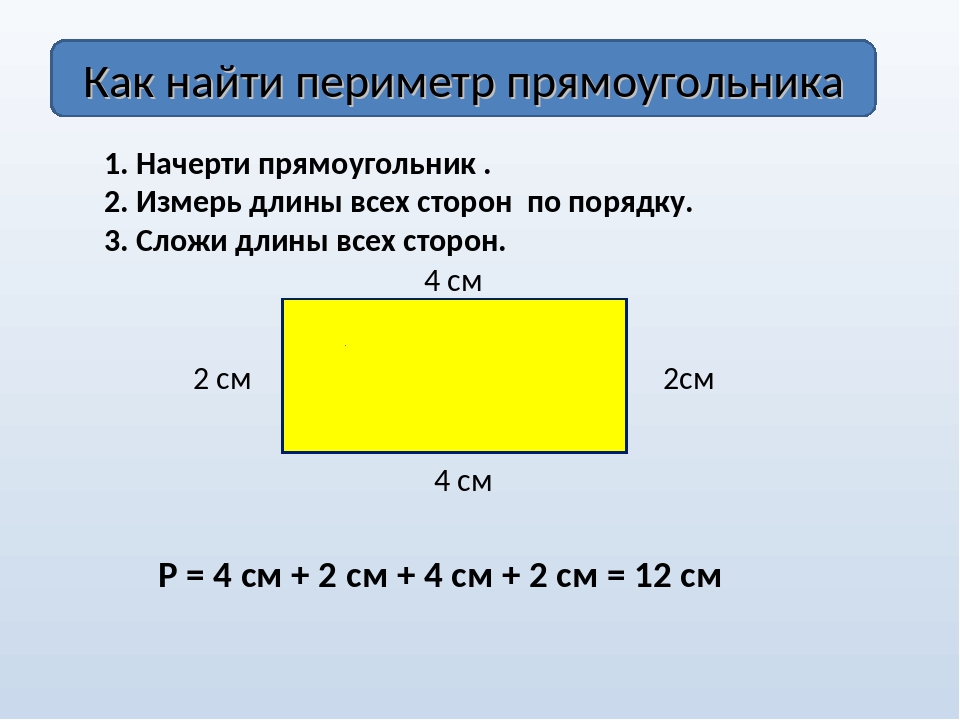 Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.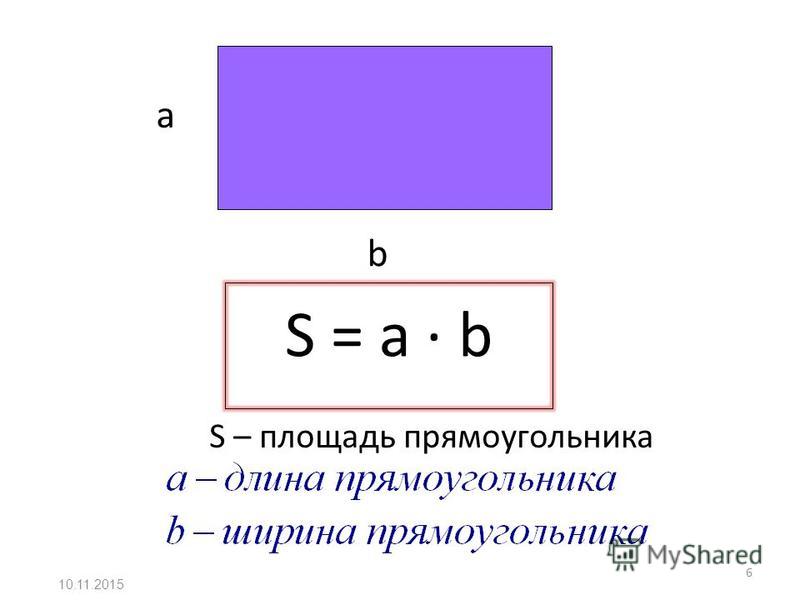
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон. Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, можно определить вторую сторону прямоугольника, воспользовавшись теоремой Пифагора. После этого задача сводится к предыдущему пункту.
Как узнать площадь прямоугольника по периметру и стороне
Периметр прямоугольника – это сумма всех его сторон. Если известен периметр прямоугольника и одна сторона (например ширина), можно вычислить площадь прямоугольника, воспользовавшись следующей формулой:
Площадь = (Периметр×ширина – ширина^2)/2.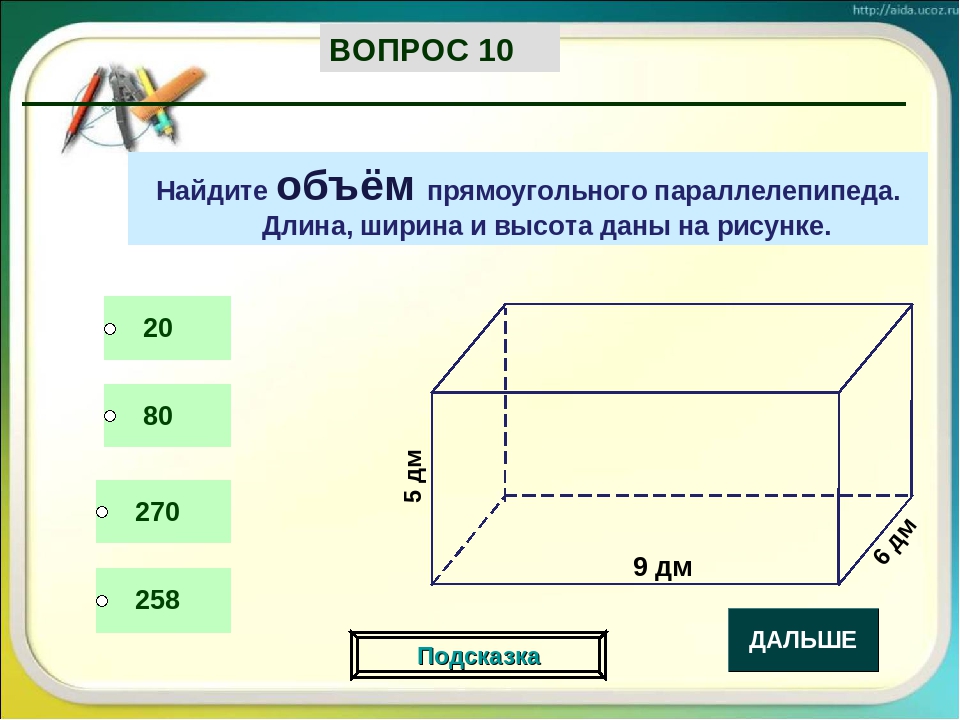 2$.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.
Что мы узнали?
Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 292.
она получится, если площадь поделить на ширину, 5 букв, сканворд
она получится, если площадь поделить на ширину
Альтернативные описания• величина, протяженность чего-нибудь
• линейный размер, протяженность
• продольный размер
• расстояние между двумя точками
• характеристика прыжка
• величина предмета
• «лежащая высота»
• главное отличие шорт от «бананов»
• что в мультфильме измеряли в попугаях, слонах и мартышках?
• вечная партнерша ширины
• величина отрезка
• габарит
• напарница ширины
• протяженность
• один из габаритов
• дополнение к ширине
• что меряют в ярдах?
• непременная характеристика всех юбок
• первое к ширине и высоте
• координата трехмерного мира
• мини и макси как величина
• площадь, деленная на ширину
• одна из трех координат
• что меряют футами?
• партнер ширины и высоты
• что измеряют в в метрах?
• . .. Волги — 3530 км
.. Волги — 3530 км
• протяжение
• что измеряют футами?
• что измеряют в метрах?
• Расстояние между двумя точками
• Продольный размер
• Протяжение, протяженность
• Величина, протяжённость чего-н. в том направлении, в к-ром две крайние точки линии, плоскости, тела лежат, в отличие от ширины, на наибольшем расстоянии друг от друга
• Линейный размер, протяженность
• … Волги — 3530 км
• «лежащая высота»
• главное отличие шорт от «бананов»
• ж. протяжение вдоль, долина; пск. долица, должина, твер. пск. длинь, перм. доль; за длину пространства, тела или вещи обычно берется направление наибольшего протяжения его; длина, ширина и вышина, или мера по уровню вдоль и поперек и мера по отвесу, составляют три основные протяжения всякого тела или пространства. Длина градуса, мера его погонною мерой, верстами, саженями и пр. длину, длиною, долиню три сажена. Эка длина какая! Длинный, большой длины, в пространстве или во времени; долгий. Весенний день длинен (долог), да нитка коротка: а осенний день короток, да нитка длинна (долга). Народ более любит слово долгий, а мы относим его почти только ко времени. Волос долог, а язык длинней (у бабы). Это еще длинна (долга) песня. Длинненький, длинноватый, длиннехо(ше)нек. длинным-длиннешенек. Длинник м. мера или протяжение в длину, длина. Лесок потянулся длинником. десятине длиннику поперечнику сажен. Брус, доска; связь или настилка в длину, вдоль; противопол. поперечник; продольное бревно, брус, жердь. Стар. батог, палка, хлыст. прут, которым наказывали. Орл. вор. узкая полоса земли, пай или участок, поле. Астрах. четырехсаженное бревно. астрах. рыбаков, длинник самоловная снасть: к веревке (хребтине) привязывают на поводцах удочек, без наживы; рыба, проходя, садится боком; два длинника составляют счал, а три длинника перетягу: сотня и более перетяг, до тыс. крючков, занимают около версты и назыв. порядком. Ставить длинники в море на чипчиках кольях), назыв. выбивать порядки.
Весенний день длинен (долог), да нитка коротка: а осенний день короток, да нитка длинна (долга). Народ более любит слово долгий, а мы относим его почти только ко времени. Волос долог, а язык длинней (у бабы). Это еще длинна (долга) песня. Длинненький, длинноватый, длиннехо(ше)нек. длинным-длиннешенек. Длинник м. мера или протяжение в длину, длина. Лесок потянулся длинником. десятине длиннику поперечнику сажен. Брус, доска; связь или настилка в длину, вдоль; противопол. поперечник; продольное бревно, брус, жердь. Стар. батог, палка, хлыст. прут, которым наказывали. Орл. вор. узкая полоса земли, пай или участок, поле. Астрах. четырехсаженное бревно. астрах. рыбаков, длинник самоловная снасть: к веревке (хребтине) привязывают на поводцах удочек, без наживы; рыба, проходя, садится боком; два длинника составляют счал, а три длинника перетягу: сотня и более перетяг, до тыс. крючков, занимают около версты и назыв. порядком. Ставить длинники в море на чипчиках кольях), назыв. выбивать порядки. Длинник м. вологодск. узкая и долгая полоса пашни. Длинняк м. собират. жердняк, шесты, жерди, слеги. Длиннота ж. длина, длинь, как свойство, состояние; более о времени, о растянутом разсказе и пр. Длинноватость ж. состояние, качество того, что длинновато, немного или чересчур длинно. Длинногривый, длнно(долго)ногий, длинноносый, длиннополый, длиннотенный, длинношерстый и пр. понятны по составу; говорят также: долгогривый, долгополый и пр. Длинноголенка, растен. Macrocnemum голенастка, переводн. Длинноголовка, растен. Erycbbe головчатка, переводн. Длинноколенка, растен. Phalangium, перeводн. коленчатка. Длиннососудка, растен. Mecardonia. Длинностручник растен. Macrolobium, переводн. Длиннотычинник, растен. Macrostemma Длинноцветник, растен. Selena. Названия эти придуманные, переводные. Длить, тянуть время, мешкать, медлить, откладывать, оттягивать, пробавляться. Он попусту длит делом, он только время длит. Длиться тянуться, продолжаться; казаться долгим, противопол. коротаться. Болезнь длится более года.
Длинник м. вологодск. узкая и долгая полоса пашни. Длинняк м. собират. жердняк, шесты, жерди, слеги. Длиннота ж. длина, длинь, как свойство, состояние; более о времени, о растянутом разсказе и пр. Длинноватость ж. состояние, качество того, что длинновато, немного или чересчур длинно. Длинногривый, длнно(долго)ногий, длинноносый, длиннополый, длиннотенный, длинношерстый и пр. понятны по составу; говорят также: долгогривый, долгополый и пр. Длинноголенка, растен. Macrocnemum голенастка, переводн. Длинноголовка, растен. Erycbbe головчатка, переводн. Длинноколенка, растен. Phalangium, перeводн. коленчатка. Длиннососудка, растен. Mecardonia. Длинностручник растен. Macrolobium, переводн. Длиннотычинник, растен. Macrostemma Длинноцветник, растен. Selena. Названия эти придуманные, переводные. Длить, тянуть время, мешкать, медлить, откладывать, оттягивать, пробавляться. Он попусту длит делом, он только время длит. Длиться тянуться, продолжаться; казаться долгим, противопол. коротаться. Болезнь длится более года. немилым часы длятся. Длительный, продолжительный, долгий, медленный, мешкотный, медлительный. Длительность ж. свойство, состояние длительного; медленность. Длитель м. -ница ж. кто медлит, тянет время: медлитель, мешкатель
немилым часы длятся. Длительный, продолжительный, долгий, медленный, мешкотный, медлительный. Длительность ж. свойство, состояние длительного; медленность. Длитель м. -ница ж. кто медлит, тянет время: медлитель, мешкатель
• что в мультфильме измеряли в попугаях, слонах и мартышках
• что измеряют в в метрах
• что измеряют в метрах
• что измеряют футами
• что меряют в ярдах
• что меряют футами
• координата трёхмерного мира
• важный параметр для юбки
Найти стороны прямоугольника известна только площадь. Периметр и площадь прямоугольника
Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко
мнаты и другое.
Геометрическая фигура
Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.
Площадь=длина*ширина
Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.
Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,
S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .
Резюме
Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.
4. Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата :
5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):
Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):
6. Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:
7. Формула радиуса окружности, которая описана около прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны у этого угла:
8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника.
Формулы для определения угла между стороной и диагональю прямоугольника:
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника.
Формулы для определения угла меж диагоналей прямоугольника:
1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:
Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ.
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника.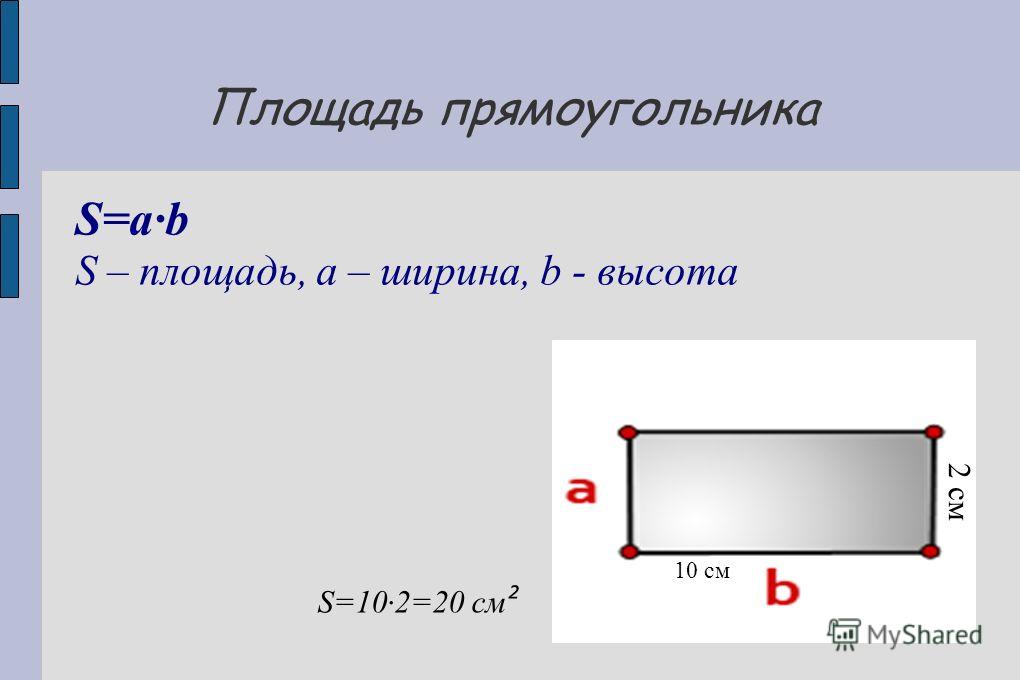 Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников.
 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника , а короткую — шириной прямоугольника .
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Шириной прямоугольника называют длину более короткой пары его сторон.Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d 2 — b 2
b = √d 2 — a 2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a 2 + b 2
2. Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = D о
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S: sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b )
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d 2 — a 2 ) = 2(b + √d 2 — b 2 )
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R 2 — a 2 ) = 2(b + √4R 2 — b 2 )
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √D o 2 — a 2 ) = 2(b + √D o 2 — b 2 )
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a √4R 2 — a 2 = b √4R 2 — b 2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a √D o 2 — a 2 = b √D o 2 — b 2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
4a, где a — сторона квадрата или ромба. Тогда длина стороны равна одной четвертой периметра: a = p/4.
Легко разрешима эта задача и для треугольника. У него три одинаковых по длине стороны , поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.
Для остальных фигур понадобятся дополнительные данные. Например, можно найти стороны , зная его периметр и площадь. Предположим, что длина двух противолежащих сторон прямоугольника равна a, а длина двух других сторон — b. Тогда периметр p прямоугольника равен 2(a+b), а площадь s равна ab. Получим систему с двумя неизвестными:
p = 2(a+b)
s = ab.Выразим из первого уравнения а: а = p/2 — b. Подставим во второе и найдем b: s = pb/2 — b². Дискриминант этого уравнения D = p²/4 — 4s. Тогда b = (p/2±D^1/2)/2.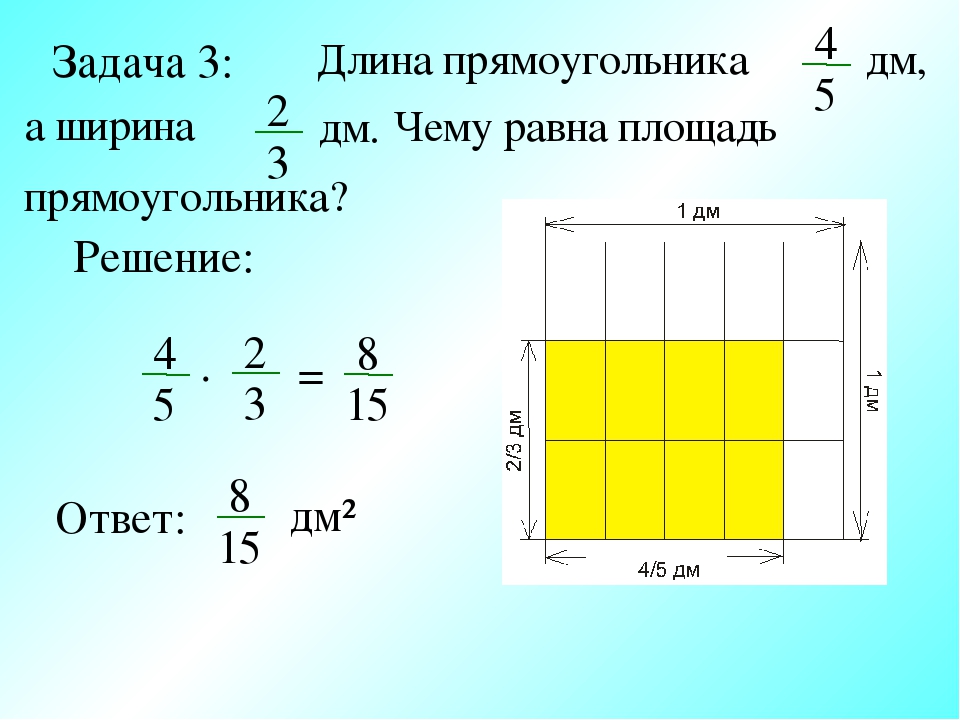 Отбросьте тот корень, который будет меньше ноля, и подставьте в для стороны a.
Отбросьте тот корень, который будет меньше ноля, и подставьте в для стороны a.
Источники:
- Найти стороны прямоугольника
Если вы знаете значение а, то вы можете сказать, что решили квадратное уравнение, потому как его корни будут найдены очень легко.
Вам понадобится
- -формула дискриминанта квадратного уравнения;
- -знание таблицы умножения
Инструкция
Видео по теме
Полезный совет
Дискриминант квадртаного уравнения может быть положительным, отрицательным, или равняться 0.
Источники:
Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Инструкция
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще.
Вам понадобится
- калькулятор, линейка
Инструкция
Чтобы измерьте длину одной из его сторон и умножьте результат измерения на три. В виде это можно записать следующим образом:
Прт = Дс * 3,
Прт – периметр треугольника,
Дс – длина любой из его сторон.
Периметр треугольника получится в тех же измерения, что и длина его стороны.
Так как равносторонний треугольник обладает высокой степенью симметрии, то для вычисления его периметра достаточно одного из параметров. Например, площади, высоты, вписанной или описанной окружности.
Если известен радиус вписанной окружности равностороннего треугольника, то для вычисления его периметра воспользуйтесь следующей формулой:
Прт = 6 * √3 * r,
где: r — радиус вписанной окружности. ¼.
¼.
Видео по теме
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон одинаковой длины и четырех прямых углов, каждый из которых равен 90°. Определение площади или периметра четырехугольника, причем любого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти умения могут стать полезными, например, во время ремонта при расчете нужного количества материалов — покрытий для пола, стен или потолка, а также для разбивки газонов и грядок и т.д.
Как изменения размеров влияют на площадь и периметр — видео и расшифровка урока
Влияние на периметр
Так что же происходит, когда размеры начинают изменяться? Вы можете узнать это, посмотрев, как уравнение использует это измерение. Например, у вас есть неправильный пятиугольник (пятиугольная фигура с прямыми сторонами разной длины), и вы хотите знать, как изменится периметр, если вы отрежете одну из сторон на дюйм.
Формула проста: периметр P = S1 + S2 + S3 + S4 + S5 , где каждый из S , где каждый из S . Если я сделаю S1 на дюйм короче, как это повлияет на P ? Краткий взгляд на формулу говорит нам, что P также станет на дюйм короче.
Если я сделаю S1 на дюйм короче, как это повлияет на P ? Краткий взгляд на формулу говорит нам, что P также станет на дюйм короче.
Что, если я уменьшу длину прямоугольника на один дюйм? Формула периметра прямоугольника: P = 2 L + 2 W . Обратите внимание, что наш член длины L умножается на 2, поэтому периметр уменьшится на два дюйма, когда мы уменьшим L на один дюйм.
Хорошо, теперь вернемся к нашему пятиугольнику, но давайте теперь сделаем его правильным пятиугольником, где все стороны имеют одинаковую длину L . Уравнение теперь P = 5 L , что означает, что если мы отрежем L на дюйм, мы уменьшим периметр этого пятиугольника на пять дюймов! Посмотрите на формулу периметра. Вы можете видеть, как изменение одного измерения влияет на периметр фигуры.
Влияние на площадь
Точно так же вы можете сказать, как изменение размера повлияет на площадь фигуры, взглянув на формулу.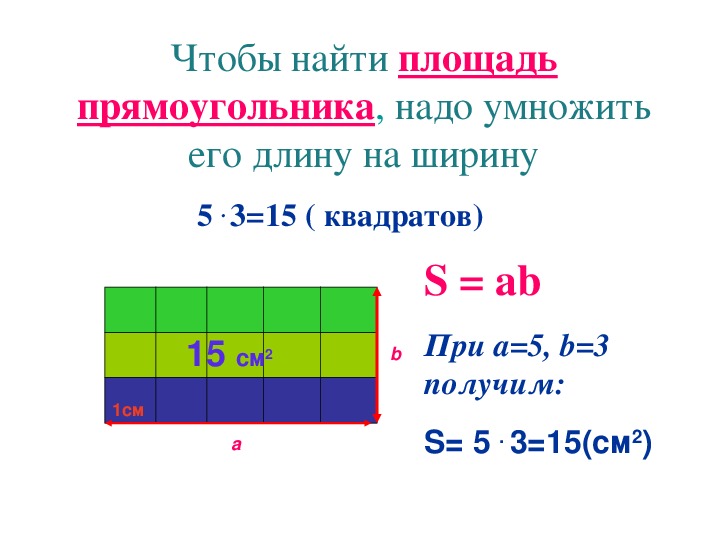 Вы должны быть осторожны с площадью, потому что это измерение поверхности, а не только длины линии. Это означает, что у вас часто будут размеры в квадрате (размеры, которые умножаются сами на себя) или размеры, которые умножаются вместе.
Вы должны быть осторожны с площадью, потому что это измерение поверхности, а не только длины линии. Это означает, что у вас часто будут размеры в квадрате (размеры, которые умножаются сами на себя) или размеры, которые умножаются вместе.
Например, площадь круга находится по формуле A = π R ². В этой формуле размер радиуса R возводится в квадрат. Поэтому, если я изменю R на , я изменю площадь фигуры на квадрат суммы, на которую я ее изменю.Если я удвою R , чтобы получить 2 R , площадь моего круга теперь станет A = π(2 R )² = 4πR²
. площади в 4 раза (она станет в четыре раза больше). Обратите внимание, что такое же изменение радиуса изменит периметр исходного круга (2π R ) только в 2 раза. Изменение размера часто оказывает большее влияние на площадь фигуры, чем на ее периметр.
Даже если размеры не возводятся в квадрат в формуле площади, они могут быть перемножены друг с другом, поэтому изменение одного измерения может оказать существенное влияние на площадь.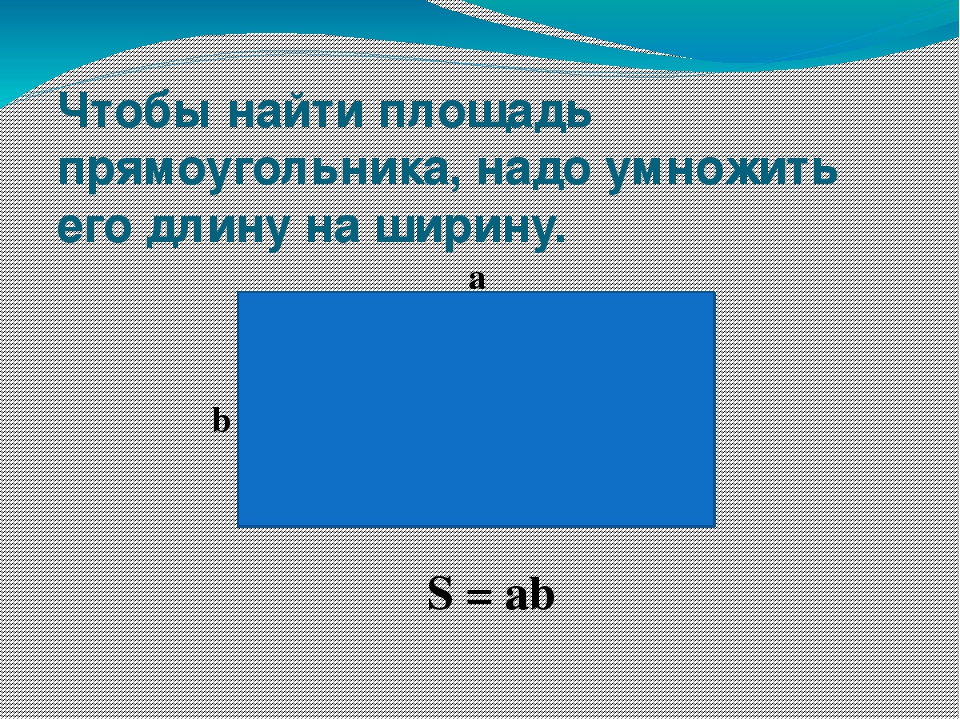 Например, площадь прямоугольника можно рассчитать, используя · = LW , где длина ·L· умножается на ширину ·W·. Это означает, что если мы уменьшим L на 2, мы фактически уменьшим площадь в два раза по сравнению с шириной W , поскольку ( L — 2) W = LW — 2 W .
Например, площадь прямоугольника можно рассчитать, используя · = LW , где длина ·L· умножается на ширину ·W·. Это означает, что если мы уменьшим L на 2, мы фактически уменьшим площадь в два раза по сравнению с шириной W , поскольку ( L — 2) W = LW — 2 W .
Резюме урока
Хорошо, давайте на минутку-другую подведем итоги. На этом уроке мы узнали, что размер является одной из измеримых характеристик, определяющих форму фигуры. Мы также узнали, что изменение одного из размеров фигуры, например длины или ширины, может оказать существенное влияние на периметр фигуры (общая длина ребра) и ее площадь (размер ). поверхности). Вы можете определить, каким будет эффект, взглянув на формулы периметра и площади любой фигуры, чтобы вычислить размер результата.Изменение размера часто оказывает большее влияние на площадь фигуры, чем на ее периметр.
словесных задач на ширину, длину и площадь
Формула площади прямоугольника такова
А знак равно ж × час
где
А
это площадь,
ж
это ширина, а
час
это высота.
Формула площади треугольника такова
А знак равно 1 2 б × час
где А это площадь, б является основой и час это высота.
Вы часто будете сталкиваться с текстовыми задачами, когда заданы два значения в одной из этих формул, а вам нужно найти третье.
Пример 1:
Прямоугольный городской квартал разделен на 56 квадратные участки одинакового размера. Если есть 14 участков по длине блока, сколько участков по ширине блока?
Это проблема площади, где «единицей» является квадратный участок.Городской квартал представляет собой прямоугольник площадью 56 , а длина 14 . Подставить в формулу.
56 знак равно ж × 14
Разделите обе части на
14
.
4 знак равно ж
Итак, городской квартал 4 участки широкие.
Пример 2:
Карлос обследует участок земли в форме прямоугольного треугольника.Площадь земли составляет 45000 квадратные метры. Если одна сторона треугольного графика 180 метров, чему равна другая сторона треугольника?
Это задача на площадь, связанная с формулой треугольника. Так как это прямоугольный треугольник, то одну сторону можно считать основанием, а другую — высотой. Заменять 45000 за А и 180 за б в формуле.
45000 знак равно 1 2 ( 180 ) час
Упрощать.
45000 знак равно 90 час
Разделите обе части на
90
.
45000 90 знак равно час
500 знак равно час
Другая сторона треугольника равна 500 метров в длину.
Длина, ширина, высота, глубина – Элементарная математика
Длина, ширина, высота, глубина
Вне уроков математики контекст обычно определяет наш выбор словаря: длина веревки, ширина дверного проема, высота флагштока, глубина бассейна.Но при описании прямоугольников или объектов в форме кирпича выбор лексики кажется менее ясным.
Вопрос: Должны ли мы обозначить два измерения прямоугольника длина и ширина ; или ширина и высота ; или даже длина и высота ? Существует ли «правильное» использование терминов длина , ширина , высота и глубина ?
Прямоугольники различной формы и положения.
Выбор лексики здесь полностью зависит от ясности и отсутствия двусмысленности. Математика не предписывает правил «правильного» использования этих терминов в данном контексте. В математике, как и везде, специализированная лексика служит для ясного и недвусмысленного общения. В этом случае наша естественная манера говорить дает нам некоторые ориентиры.
Длина: Если вы решите использовать слово длина , оно должно относиться к самому длинному измерению прямоугольника.Подумайте, как бы вы описали расстояние вдоль дороги: это длинное расстояние, длина дороги. (Слова вдоль , длина и длина th связаны друг с другом.) Расстояние поперек дороги говорит о том, насколько ширина дорога с одной стороны до другой. Это ширина дороги. (Слова wid e и wid th тоже связаны между собой.)
Когда прямоугольник нарисован на странице «наклонным», как этот, обычно проще всего обозначить длинную сторону как «длину», а другую сторону как «ширину», как если бы вы маркировали дорогу.
Наклонный прямоугольник.
Высота: Когда прямоугольник нарисован с горизонтальной и вертикальной сторонами, слово высота дает понять, какой размер имеется в виду; высота обозначает, как высота (какая высота) прямоугольника. Это позволяет легко указать другое измерение — как ширина прямоугольника от стороны до стороны — с помощью слова ширина . И если поперечный размер больше, чем высота, также допустимо называть его длиной прямоугольника, так как это не создает путаницы.
Прямоугольники различной ориентации.
Обратите внимание, что в этом случае, когда используется высота , сравнительный размер не имеет значения. Поскольку высота всегда вертикальна, размеры, ширина или высота могут быть больше.
Когда слово высота используется в сочетании с основание , оно имеет особое значение, которое не обязательно относится к вертикальному измерению.
Для некоторых непрямоугольных форм термины длина , высота или ширина остаются неясными, ясно показывают, что вы имеете в виду, и ссылаются на это как на «это расстояние» или «это измерение».
Три измерения
При наименовании размеров трехмерной фигуры единственное правило: иметь смысл и быть ясным . Это поможет использовать ярлыки.
Когда фигура «ровная», высота явно относится к вертикальному измерению — насколько высока фигура — независимо от того, является ли это измерение наибольшим, наименьшим или чем-то средним; длина (если вы используете это слово) относится к большему из двух других измерений. Но вы также можете ссылаться на другие размеры как ширина и глубина (и они в значительной степени взаимозаменяемы, в зависимости от того, что «кажется» широким или глубоким в фигуре).См. эти примеры.
Когда высота неясна — например, если фигура не «ровная» — люди не могут знать, что подразумевается под шириной, глубиной или высотой без меток, хотя длина обычно по-прежнему считается относящейся к самому длинному измерению на фигура.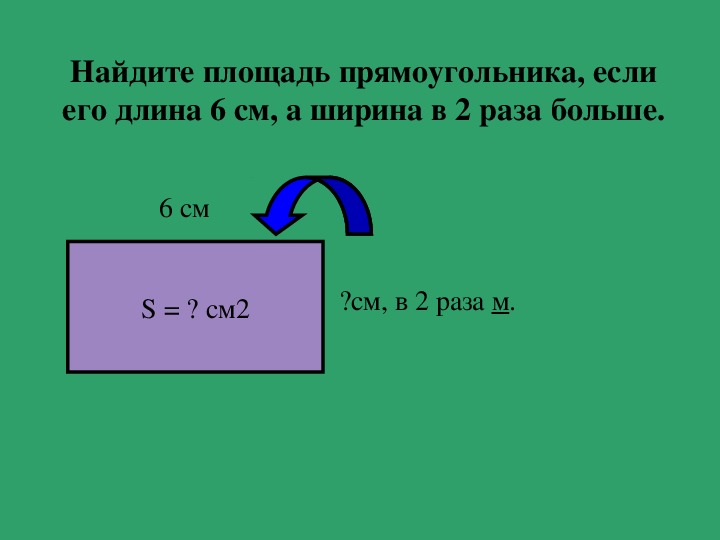 И, как и в случае с двумя измерениями, такие термины, как «длина», «ширина» и «высота», не будут казаться естественными или понятными для некоторых форм, таких как теннисный мяч.
И, как и в случае с двумя измерениями, такие термины, как «длина», «ширина» и «высота», не будут казаться естественными или понятными для некоторых форм, таких как теннисный мяч.
Что в слове?
Длина , Ширина , Высота и Глубина являются существительными производными от прилагательных длинный , широкий , высокий и Они следуют общепринятому английскому образцу, который включает изменение гласной (часто на более короткую гласную) и добавление th . (Одинокий t в height является современным. Устаревшие формы включают heighth и highth , и до сих пор часто можно услышать, как люди произносят это таким образом.)
| ш я г е | д ее р | ч я г | л или нг | бр оа д |
| ш и д ч | д е р й | h ei gh т | л е нг й | br шт. d th d th |
Другие пары прилагательное-существительное в английском языке также связаны таким же образом: e.г., hale как «здоровый и крепкий» и health (но hale , за исключением этого выражения, теперь чаще всего заменяется на «здоровый»).
Как изменится площадь прямоугольника, если его длину и ширину увеличить вдвое? – М.В.Организинг
Как изменится площадь прямоугольника, если его длину и ширину увеличить вдвое?
Ответ. (1) площадь удвоится, если длина удвоится, а ширина останется прежней. как мы видим, 16 вдвое больше 8, поэтому площадь увеличивается в 4 раза.2 размер увеличивается в 4 раза.
Что произойдет с площадью прямоугольника, если его длину и ширину увеличить вдвое, а длину увеличить вдвое, а ширину утроить?
Ответ — Площадь прямоугольника в 6 раз больше.
Как удвоение длин сторон прямоугольника влияет на его площадь?
Ответ проверен экспертом Если удвоить длину сторон, площадь умножится на четыре. Ясно, что площадь будет x*y=xy. У нового прямоугольника длины сторон будут 2x и 2y, а значит, площадь 2x*2y=4xy.4xy/xy=4 – следовательно, площадь нового прямоугольника в четыре раза больше площади старого.
Ясно, что площадь будет x*y=xy. У нового прямоугольника длины сторон будут 2x и 2y, а значит, площадь 2x*2y=4xy.4xy/xy=4 – следовательно, площадь нового прямоугольника в четыре раза больше площади старого.
Как найти длину и ширину, если известны площадь и периметр?
Пусть P периметр прямоугольника, а A его площадь. Пусть W и L будут соответственно шириной и длиной прямоугольника. Найдите W и L через P и A. Решите приведенное выше уравнение для L и найдите W, используя W = P / 2 – L.
Есть ли связь между площадью и периметром?
В чем разница между периметром и площадью фигуры? Периметр – это сумма длин всех сторон фигуры.Площадь — это количество двухмерного пространства, которое занимает фигура.
Могут ли два прямоугольника иметь одинаковый периметр, но разные площади?
На этом уроке вы узнаете, что прямоугольники могут иметь одинаковый периметр, но разную площадь, путем построения прямоугольников и организации информации на диаграмме.
Может ли периметр быть больше площади?
Периметр всегда больше, кроме одного (форма G). Площадь и периметр одинаковы. То же самое произошло, если у вас есть прямоугольник, длина которого равна 6, а ширина — 3.В таблице 3 (свою школу они не указали) рассматривалась задача найти фигуру, периметр которой в численном выражении вдвое больше площади.
Сможете ли вы найти периметр прямоугольника, если знаете его площадь?
Невозможно определить периметр прямоугольника, зная только его площадь. Площадь прямоугольника зависит от двух неизвестных, длины и ширины, поэтому необходимо знать хотя бы одну сторону прямоугольника вместе с площадью, чтобы определить другую сторону и, таким образом, периметр.
Что такое периметр и площадь?
О стенограмме.Периметр — это расстояние вокруг внешней стороны фигуры. Площадь измеряет пространство внутри фигуры.
Как найти периметр с площадью?
Разделите периметр на 4: это даст вам длину одной стороны. Затем возведите эту длину в квадрат: это даст вам площадь. В этом примере 14 ÷ 4 = 3,5. (3,5)² = 12,25 квадратных футов.
Затем возведите эту длину в квадрат: это даст вам площадь. В этом примере 14 ÷ 4 = 3,5. (3,5)² = 12,25 квадратных футов.
Какие формулы для периметра и площади?
Формула для геометрических фигур
| Формула периметра | |
|---|---|
| Квадрат | 4 × сторона |
| Формула площади | |
| Квадрат | сторона2 |
| Прямоугольник | длина × ширина |
Почему важны площадь и периметр?
Периметр и площадь.Периметр и площадь — две важные и фундаментальные математические темы. Они помогают вам количественно определить физическое пространство, а также обеспечивают основу для более сложной математики, которую можно найти в алгебре, тригонометрии и исчислении.
Что такое примеры периметра и площади?
Например, чтобы оградить сад у вашего дома, необходимая длина материала для ограждения равна периметру сада. Если это квадратный сад, каждая сторона которого равна см, то периметр будет равен 4а см. Площадь — это пространство, содержащееся в фигуре или заданной фигуре.
Если это квадратный сад, каждая сторона которого равна см, то периметр будет равен 4а см. Площадь — это пространство, содержащееся в фигуре или заданной фигуре.
Как найти площадь и периметр любой фигуры?
Периметр — это длина контура фигуры. Чтобы найти периметр прямоугольника или квадрата, нужно сложить длины всех четырех сторон. x в данном случае — длина прямоугольника, а y — ширина прямоугольника. Площадь – это измерение поверхности фигуры.
Зачем нужна площадь?
Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
Почему мы учим студентов вычислять площадь и периметр?
Единицы измерения площади и периметра важны для математики, поскольку они являются физическими аспектами математики. Изучение площади и периметра даст учащимся возможность использовать математику, которая нужна и используется реальными людьми за пределами школы.
Где мы используем площадь и периметр в нашей повседневной жизни?
Использование периметра и площади в повседневной жизни
- Ограждение участка под посев.Поскольку заборы стоят денег для данной области, вы хотели бы минимизировать периметр.
- Планирование строительства дома.
- Строительство сарая с стойлами для лошадей.
- Дерево.
- Строительство бассейна.
Каково значение периметра в реальной жизни?
Мы часто находим периметр, когда зажигаем рождественские гирлянды вокруг дома или ограждаем сад на заднем дворе. Другие примеры могут включать в себя нахождение общей длины границы футбольного поля или длины вязания крючком или ленты, необходимой для покрытия границы настольного коврика.
Где мы используем площадь в реальной жизни?
Какие ситуации в реальной жизни требуют от нас использования площади? ▫ Напольные покрытия, такие как ковры и плитка, требуют измерения площади. Обои и краска также требуют измерения площади. Ткань, используемая для одежды и других предметов, также требует учета длины и ширины.
Обои и краска также требуют измерения площади. Ткань, используемая для одежды и других предметов, также требует учета длины и ширины.
Кто использует периметр в своей работе?
Многие задания используют atea и периметр, например; Геодезия, оценка полов, архитектура, машиностроение, этот список можно продолжать и продолжать.
Кто использует геометрию в реальной жизни?
Применение геометрии в реальном мире включает автоматизированное проектирование строительных чертежей, проектирование сборочных систем в производстве, нанотехнологии, компьютерную графику, визуальные графики, программирование видеоигр и создание виртуальной реальности.
Когда вам нужно найти периметр чего-либо?
Периметр — это длина контура фигуры. Чтобы найти периметр прямоугольника или квадрата, нужно сложить длины всех четырех сторон.x в данном случае — длина прямоугольника, а y — ширина прямоугольника.
Для каких работ требуется геометрия?
Информация о карьере для работы, связанной с геометрией
- Архитектор.

- Картограф и фотограмметрист.
- Составитель.
- Инженер-механик.
- Сюрвейер.
- Городской и региональный планировщик.
Используют ли врачи геометрию?
В области медицины геометрия помогает врачам понять, как решить определенные медицинские проблемы.Глядя на то, как геометрия используется в физиотерапии, работе с телом и в медицинских технологических достижениях, мы увидим, как геометрия играет ключевую роль в области медицины.
Нужна ли в жизни геометрия?
Геометрия помогает нам решить, какие материалы использовать, какой дизайн сделать, а также играет жизненно важную роль в самом процессе строительства. Различные дома и здания строятся в разных геометрических формах, чтобы придать новый вид, а также обеспечить надлежащую вентиляцию внутри дома.
Кто отец геометрии?
Евклид
Видео-вопрос: нахождение длины прямоугольника по его площади и ширине путем деления двух многочленов с последующим вычислением его периметра
Стенограмма видео
Площадь прямоугольника равна 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10 квадратных сантиметров, а ширина равна 𝑦 плюс два сантиметра.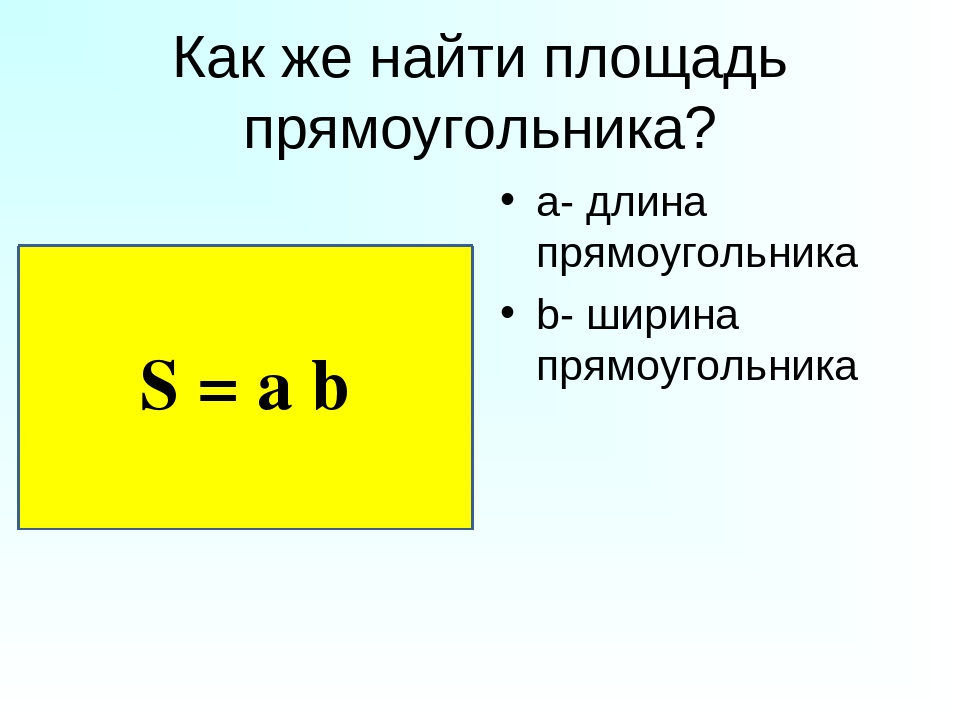 Найдите его длину через 𝑦 и его периметр, когда 𝑦 равно четырем.
Найдите его длину через 𝑦 и его периметр, когда 𝑦 равно четырем.
Площадь прямоугольника вычисляется путем умножения длины на ширину. Если мы допустим длину прямоугольника равной 𝑥 сантиметров, то 𝑥, умноженное на 𝑦 плюс два, должно быть равно 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10. Деление обеих сторон на 𝑦 плюс два позволяет нам вычислить длину путем деления 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10 на 𝑦 плюс два.
Теперь мы собираемся использовать деление в длину, чтобы вычислить длину прямоугольника. Чтобы разделить 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10, кубическое, на 𝑦 плюс два, линейное выражение, нам нужно делить, умножать и вычитать.Во-первых, нам нужно разделить 𝑦 в кубе на 𝑦. Это дает нам 𝑦 в квадрате. Во-вторых, нам нужно умножить это 𝑦 в квадрате на 𝑦 плюс два, чтобы получить остаток. 𝑦 в квадрате, умноженное на 𝑦, равно 𝑦 в кубе, а 𝑦 в квадрате, умноженное на два, равно двум 𝑦 в квадрате.
Наш следующий шаг — вычесть эти две строки. Ну, 𝑦 в кубе минус 𝑦 в кубе равно нулю. И в этом случае два 𝑦 в квадрате минус два 𝑦 в квадрате тоже равно нулю. Поэтому остатка нет. Это означает, что нам не нужно делить член в квадрате 𝑦 на 𝑦.Таким образом, мы можем отбросить пять 𝑦 плюс 10. Теперь мы повторим процесс, разделив пять 𝑦 на 𝑦. Ну, так как пять 𝑦 разделить на 𝑦 равно пяти, мы можем поставить пять в строке ответа. Умножение этих пяти на 𝑦 плюс два дает нам пять 𝑦 плюс 10, так как пять умножить на 𝑦 равно пяти 𝑦, а пять умножить на два равно 10. пять 𝑦 минус пять 𝑦 равно нулю, и 10 минус 10 тоже равно нулю. Следовательно, мы можем сказать, что 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10 разделить на 𝑦 плюс два равно 𝑦 в квадрате плюс пять.Следовательно, длина прямоугольника равна 𝑦 в квадрате плюс пять. В конце этого видео я покажу вам альтернативный метод расчета длины с точки зрения 𝑦. Однако сейчас мы сосредоточимся на второй части вопроса: нахождении периметра.
Ну, 𝑦 в кубе минус 𝑦 в кубе равно нулю. И в этом случае два 𝑦 в квадрате минус два 𝑦 в квадрате тоже равно нулю. Поэтому остатка нет. Это означает, что нам не нужно делить член в квадрате 𝑦 на 𝑦.Таким образом, мы можем отбросить пять 𝑦 плюс 10. Теперь мы повторим процесс, разделив пять 𝑦 на 𝑦. Ну, так как пять 𝑦 разделить на 𝑦 равно пяти, мы можем поставить пять в строке ответа. Умножение этих пяти на 𝑦 плюс два дает нам пять 𝑦 плюс 10, так как пять умножить на 𝑦 равно пяти 𝑦, а пять умножить на два равно 10. пять 𝑦 минус пять 𝑦 равно нулю, и 10 минус 10 тоже равно нулю. Следовательно, мы можем сказать, что 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10 разделить на 𝑦 плюс два равно 𝑦 в квадрате плюс пять.Следовательно, длина прямоугольника равна 𝑦 в квадрате плюс пять. В конце этого видео я покажу вам альтернативный метод расчета длины с точки зрения 𝑦. Однако сейчас мы сосредоточимся на второй части вопроса: нахождении периметра.
Поскольку теперь мы знаем ширину и длину прямоугольника, мы можем подставить значение 𝑦 равное четырем, чтобы вычислить его периметр. Ширина прямоугольника четыре плюс два, что равно шести сантиметрам. А длина равна четырем в квадрате плюс пять, что равно 21 сантиметру, так как четыре в квадрате равно 16, а 16 плюс пять равно 21.Чтобы вычислить периметр любой фигуры, нам нужно вычислить расстояние вокруг внешней стороны фигуры. В этом случае нам нужно добавить 21, шесть, 21 и шесть.
Ширина прямоугольника четыре плюс два, что равно шести сантиметрам. А длина равна четырем в квадрате плюс пять, что равно 21 сантиметру, так как четыре в квадрате равно 16, а 16 плюс пять равно 21.Чтобы вычислить периметр любой фигуры, нам нужно вычислить расстояние вокруг внешней стороны фигуры. В этом случае нам нужно добавить 21, шесть, 21 и шесть.
Сложение этих четырех чисел дает нам 54 сантиметра. Следовательно, периметр прямоугольника равен 54 сантиметрам. Следовательно, если площадь прямоугольника равна 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10, а ширина равна 𝑦 плюс два, его длина равна 𝑦 в квадрате плюс пять. А периметр, когда 𝑦 равно четырем, равен 54 сантиметрам. Теперь мы рассмотрим альтернативный метод нахождения выражения длины через 𝑦.
Поскольку площадь прямоугольника вычисляется путем умножения ширины на длину, мы знаем, что в этом случае 𝑦 плюс два умножить на что-то равно 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10. Так как 𝑦 плюс два равно линейное уравнение и 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10 является кубическим уравнением, отсутствующий член, в данном случае длина, должен быть квадратным выражением, поскольку линейное выражение, умноженное на квадратное выражение, дает нам кубическое выражение.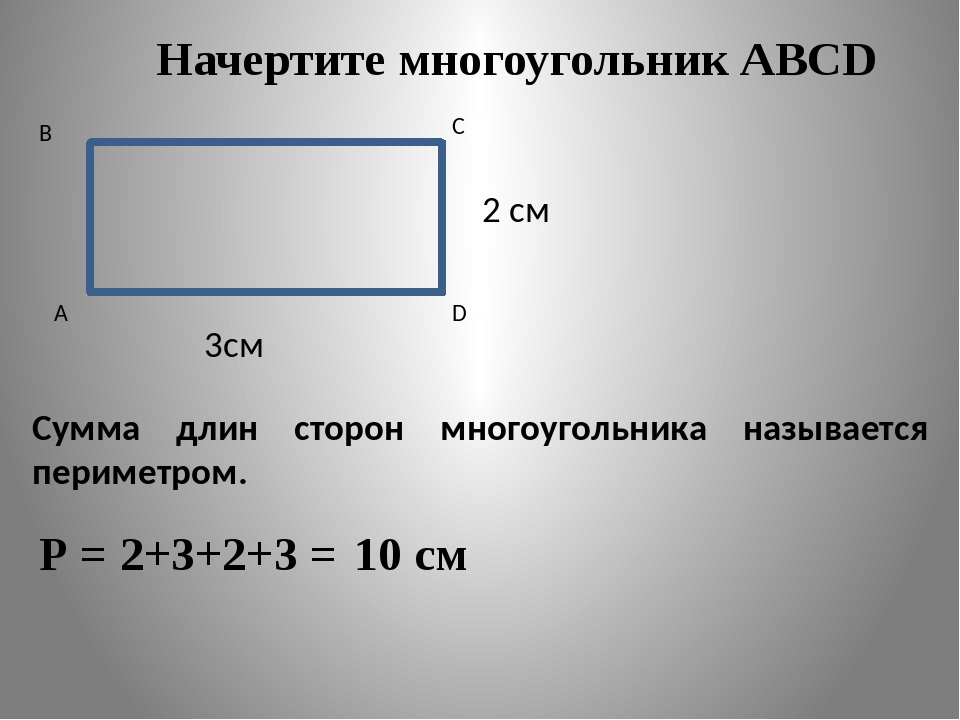
Рассматривая общее квадратное выражение 𝑎𝑦 в квадрате плюс 𝑏𝑦 плюс 𝑐, мы можем видеть, что 𝑦 плюс два, умноженные на это квадратное выражение, дают 𝑦 в кубе плюс два 𝑦 в квадрате плюс пять 𝑦 плюс 10.Расширение при умножении скобок или круглых скобок дает нам 𝑎𝑦 в кубе плюс 𝑏𝑦 в квадрате плюс 𝑐𝑦, когда мы умножаем квадратное число на 𝑦, и два 𝑎𝑦 в квадрате плюс два 𝑏𝑦 плюс два 𝑐, когда мы умножаем квадратное число на два. Мы знаем, что это должно быть равно кубическому выражению для нашей площади.
Сравнение коэффициентов дает нам четыре уравнения. Для 𝑦 в кубе 𝑎 равно единице. Для 𝑦 в квадрате 𝑏 плюс два 𝑎 равно двум. Для терминов 𝑦 𝑐 плюс два 𝑏 равно пяти. А для бесплатных терминов два 𝑐 равняются 10.Итак, первое уравнение говорит нам, что 𝑎 равно единице. А деление четвертого уравнения на два говорит нам, что 𝑐 равно пяти. Теперь мы можем подставить эти два значения во второе или третье уравнение, чтобы вычислить значение 𝑏.
Так как пять плюс два 𝑏 равно пяти, 𝑏 должно быть равно нулю.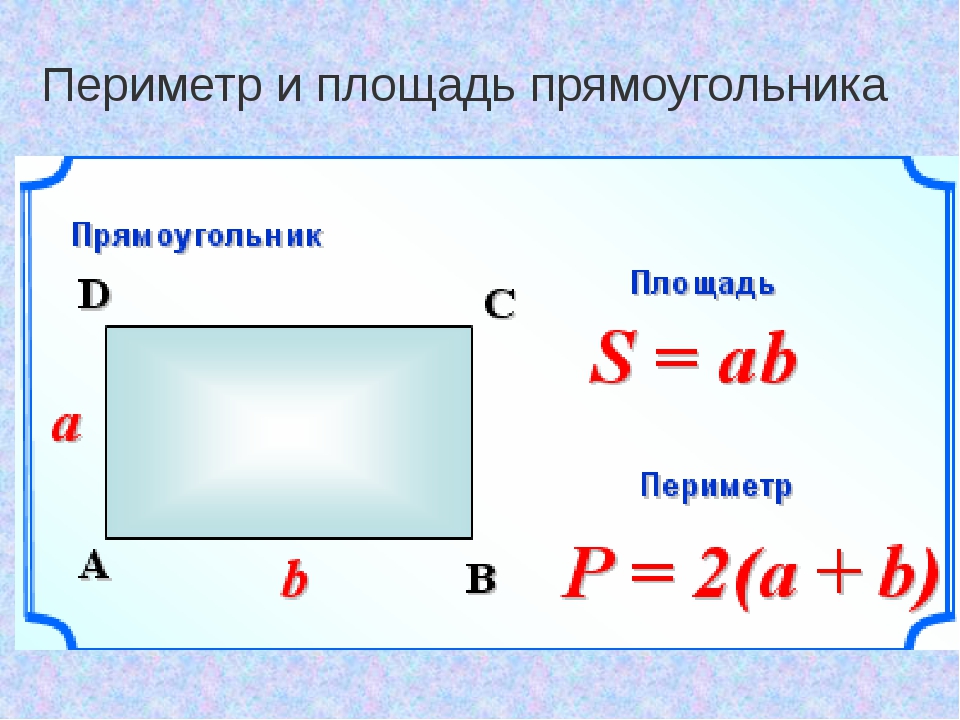 Подставив их обратно в наше квадратное выражение, мы получим один 𝑦 в квадрате плюс ноль 𝑦 плюс пять. Это можно упростить, чтобы получить выражение для длины 𝑦 в квадрате плюс пять.Это всего лишь несколько разных способов найти длину с точки зрения 𝑦.
Подставив их обратно в наше квадратное выражение, мы получим один 𝑦 в квадрате плюс ноль 𝑦 плюс пять. Это можно упростить, чтобы получить выражение для длины 𝑦 в квадрате плюс пять.Это всего лишь несколько разных способов найти длину с точки зрения 𝑦.
Какая связь между длиной и шириной прямоугольника? – Реабилитацияроботикс.нет
Какая связь между длиной и шириной прямоугольника?
Площадь прямоугольника равна произведению ширины и длины прямоугольника. A = L * W, где A — площадь, L — длина, W — ширина или ширина.
Какова связь между площадью прямоугольника и его сторонами?
Площадь прямоугольника на самом деле является произведением его сторон на его длину и ширину.Таким образом, формула вычисления площади прямоугольника такова: A = l x w или A = lw.
Есть ли связь между площадью и периметром прямоугольника?
Между периметром прямоугольника и его площадью нет прямой зависимости.
Какая связь между длиной и площадью?
Длина — это размер отрезка (см. формулы расстояний), площадь — это размер замкнутой области на плоскости, а объем — это размер твердого тела.
формулы расстояний), площадь — это размер замкнутой области на плоскости, а объем — это размер твердого тела.
Длина стороны и площадь пропорциональны?
Поскольку стороны представляют собой длину, а длины являются одномерными, соотношение сторон не будет предсказывать соотношение площадей.Чтобы найти отношения площадей, возведите отношение длин сторон во вторую степень. Это применимо, потому что площадь является квадратным или двумерным свойством.
Как узнать длину и ширину?
Чтобы найти ширину, умножьте полученную длину на 2 и вычтите результат из периметра. Теперь у вас есть общая длина оставшихся двух сторон. Это число, деленное на 2, и есть ширина.
Как вы объясните ширину?
Определение ширины
- 1: горизонтальное измерение, проведенное под прямым углом к длине: ширине.
- 2 : масштабность или охват.
- 3 : отмеренный и отрезанный кусок материала шириной с бязь.
Какая ширина глубина и высота?
Например, размер прямоугольной комнаты на чертеже 14 футов 11 дюймов X 13 футов 10 дюймов соответствует размеру комнаты 14 футов, 11 дюймов в ширину и 13 футов, 10 дюймов в длину. Размеры выражаются как ширина на длину на высоту или глубину в трехмерном пространстве.
Размеры выражаются как ширина на длину на высоту или глубину в трехмерном пространстве.
Что такое глубина и ширина изделия?
Глубина продукта: относится к количеству подкатегорий в линейке продуктов.Ширина продукта: это относится к количеству линеек продуктов в ассортименте. Глубина продукта: это относится к подклассам, которые могут быть получены в продуктах в отдельной линейке продуктов или классах в пределах длины продукта.
Могу ли я округлить свой рост?
Технически неправильно округлять в большую сторону, когда ваш рост составляет всего 1/4 дюйма. Вы должны, технически, округлить вниз. Впрочем, уверяю вас, никому не будет дела до того, что вас арестуют. Если бы у меня было точно 4 фута 11 дюймов, я бы, вероятно, сказал, что достаточно близко, и округлил бы.
Утром вы стали на 2 дюйма выше?
Когда мы лежим в состоянии покоя, позвоночник, как говорят, «растягивается» или разжимается, поэтому, когда мы просыпаемся утром, мы становимся выше после того, как пролежали в постели всю ночь. …
…
На сколько вы теряете рост в течение дня?
Да, это нормально. Это называется компрессией позвоночника. Ваш позвоночник разжимается во время сна, поэтому вы просыпаетесь выше, чем засыпаете, теряя в среднем полдюйма или около того примерно через два-три часа после пробуждения после полноценного ночного сна (8–10 часов или более). так).
Как найти длину, ширину, высоту и площадь? – Greedhead.net
Как найти длину, ширину, высоту и площадь?
Простейшие (и наиболее часто используемые) расчеты площади для квадратов и прямоугольников. Чтобы найти площадь прямоугольника, умножьте его высоту на ширину. Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь.
Как найти площадь основания коробки?
Узнайте все о коробке
- Коробка чаще всего характеризуется высотой h, шириной W и длиной L.
- Ширина, высота и длина коробки могут быть разными.

- Объем или количество места внутри коробки: h × W × L.
- Площадь внешней поверхности коробки равна 2(В × Ш) + 2(В × Д) + 2(Ш × Д)
Как найти ширину основания?
Чтобы найти ширину, умножьте полученную длину на 2 и вычтите результат из периметра. Теперь у вас есть общая длина оставшихся двух сторон. Это число, деленное на 2, и есть ширина.
Как найти длину, ширину и высоту коробки, зная ее объем?
Разделите объем на произведение длины и ширины, чтобы вычислить высоту прямоугольного объекта. В этом примере прямоугольный объект имеет длину 20, ширину 10 и объем 6000. Произведение 20 и 10 равно 200, а 6000 разделить на 200 дает 30. Высота объекта равна 30.
Как найти длину, зная площадь и ширину?
Чтобы сначала вычислить длину и ширину прямоугольника, вычислите значение ширины «w», используя формулу площади прямоугольника, то есть «w = A/l».
Как найти основание фигуры?
Поверхность, на которой стоит твердый объект, или нижняя линия формы, например треугольника или прямоугольника. Но вершина также называется основанием, когда она параллельна низу!
Но вершина также называется основанием, когда она параллельна низу!
Как определить объем коробки?
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если коробка 5х7х2 см, то объем коробки 70 кубических сантиметров.
Где находится основание треугольника?
Основание — это сторона треугольника, которая считается основанием, а высота треугольника — это перпендикуляр, опущенный на его основание из вершины, противоположной основанию.
.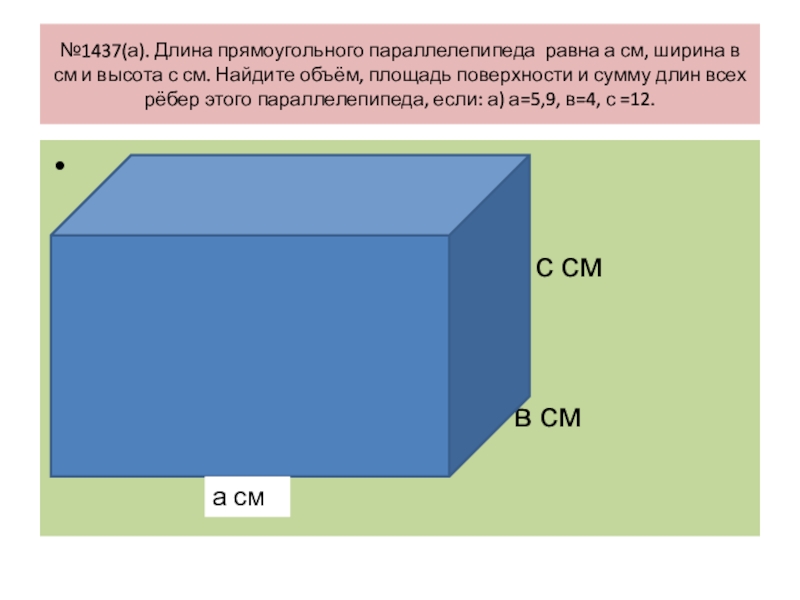

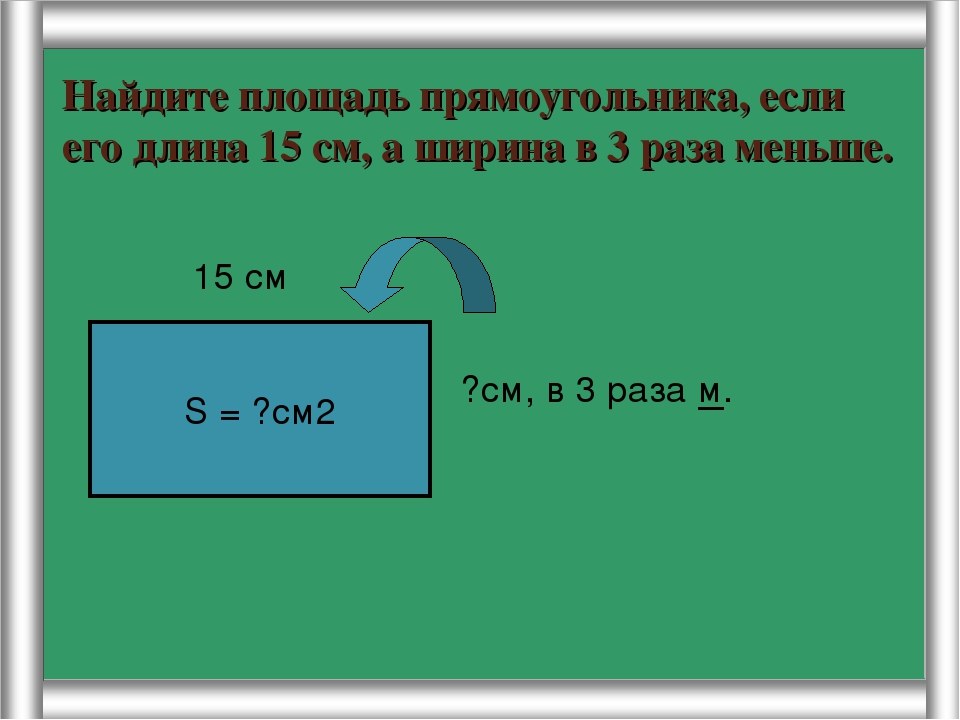 Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
