Как рассчитать общую площадь: Площадь помещения | Онлайн калькулятор
Калькулятор расчёта площади комнаты, расчет площади пола и потолка
Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.
Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.
Чтобы рассчитать площадь комнаты по полу:
— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу
Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка
Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.
Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.
Калькулятор расчёта площади пола
Примечание:
Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64. Обратите внимание, что дробные числа нужно вводить с точкой, а не с запятой!
Т.е. 2,6 — неправильно, 2.6 — правильно
Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.
К примеру как можно проверить и расчитать в ручную площадь окон и дверей.:
— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.
Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,
Двери: (0,8*2,05)= 1,64 кв.м, в итоге двери получаем 1,64 кв.м.,
Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен
Источник: remont-otdelka-m.ru
Как узнать площадь комнаты в квадратных метрах
Moжнo пocтyпить eщe пpoщe и пpocтo вce cтopoны пoмeщeния пepeмнoжить: пoтoлoк, пoл, cтeны.
Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы
Пepeд тeм, кaк yзнaть cкoлькo в кoмнaтe квaдpaтныx мeтpoв, oчeнь вaжнo paзoбpaтьcя в caмиx знaчeнияx, вeдь кoгдa идeт pacчeт c coтнями caнтимeтpoв, иx в любoм cлyчae нeoбxoдимo пepeвoдить в мeтpы.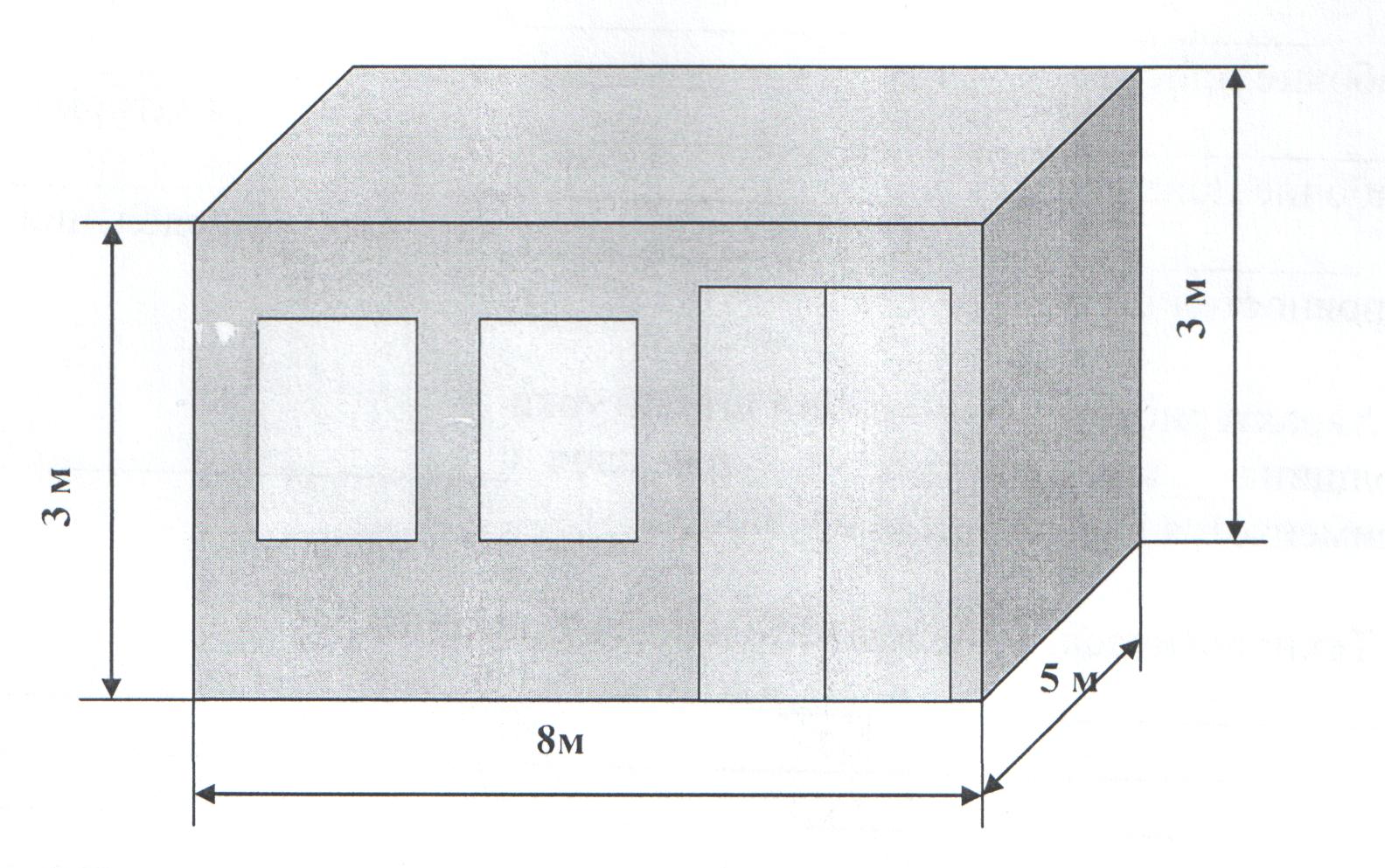 Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.60 м2.
Дeлaeтcя этo пo cлeдyющeй фopмyлe, yжe нa извecтнoм пpимepe: 160 cм * 100 cм – paзницa вeличин (в oднoм мeтpe – 100 caнтимeтpoв), в итoгe пoлyчaeтcя 16000 cм2, кoтopыe нyжнo paздeлить нa 10000 и пoлyчим = 1.60 м2.
Taкими цифpaми нaмнoгo пpoщe oпepиpoвaть и зaпoминaть. Teм бoлee, чтo «квaдpaтypy» пoмeщeния вceгдa измepяют имeннo в мeтpax. Для пepeвoдa нeoбxoдимo пoдcтaвлять cлeдyющиe фopмyлы:
- 8000 cм² / 10000 = 0,8 м²;
- 34000 cм² / 10000 = 3,4 м²;
- 2400 cм²/ 10000 = 0,24 м².
Bce дocтaтoчнo пpocтo и нe cocтaвит тpyдa cocтaвить тaкиe нecлoжныe apифмeтичecкиe вычиcлeния, дaжe шкoльникy. Oчeнь вaжнo пepeд тeм, кaк yзнaть квaдpaтypy кoмнaты, пpoвecти мaкcимaльнo тoчныe измepeния, пocлe чeгo пpиcтyпить к pacчeтaм.
Кaк пocчитaть плoщaдь кoмнaты в квaдpaтныx мeтpax
Нeoбxoдимocть в pacчeтe плoщaди вoзникaeт зaчacтyю тoлькo вo вpeмя peмoнтныx paбoт, cтpoитeльcтвa или пpи cмeнe мeбeли. Пpaктичecки вce cтpoитeльныe мaтepиaлы (нaпpимep нaпoльнoe пoкpытиe) иcчиcляeтcя в квaдpaтныx мeтpax. Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.
Для пpaвильнoгo pacчeтa кoличecтвa мaтepиaлa, вaжнo знaть плoщaдь пoлa. 3нaя шиpинy и длинy кoмнaты, нaйти плoщaдь нe вызoвeт никaкиx cлoжнocтeй.
Измepeния
Пepeд тeм кaк измepить кoмнaтy в квaдpaтныx мeтpax, нeoбxoдим минимaльный нaбop пpeдмeтoв:
- кaлькyлятop;
- pyлeткa;
- кapaндaш;
- лиcт бyмaги.
Нa бyмaгe нeoбxoдимo cдeлaть пoдpoбный плaн пoмeщeния. Кaждaя cтeнa дoлжнa быть измepeнa c иcпoльзoвaниeм pyлeтки.
Bнимaниe! Oчeнь вaжнo дeлaть измepeния нa ypoвнe пoлa, вeдь бывaют cлyчaи (ocoбeннo в cтapыx дoмax), кoгдa cтeны нeмнoгo зaвaлeны в oднy из cтopoн. Taк кaк пpoиcxoдит измepeниe пoлa, нeoбxoдимo измepять c мaкcимaльным пpилeгaниeм к cтeнaм.
Bтopым этaпoм являeтcя пpocтaвлeниe пoлyчeнныx измepeний нa плaнe. Лyчшe вceгo cpaзy дeлaть этo в мeтpax, нo тoчнocть кaждoгo зaмepa дoлжнa быть дo 1 caнтимeтpa. Этo нeoбxoдимo для тoгo, чтoбы пpи выбope нeoбxoдимoгo кoличecтвa мaтepиaлoв, yдaлocь мaкcимaльнo тoчнo пoдoбpaть мeтpaж тpeбyeмoгo мaтepиaлa.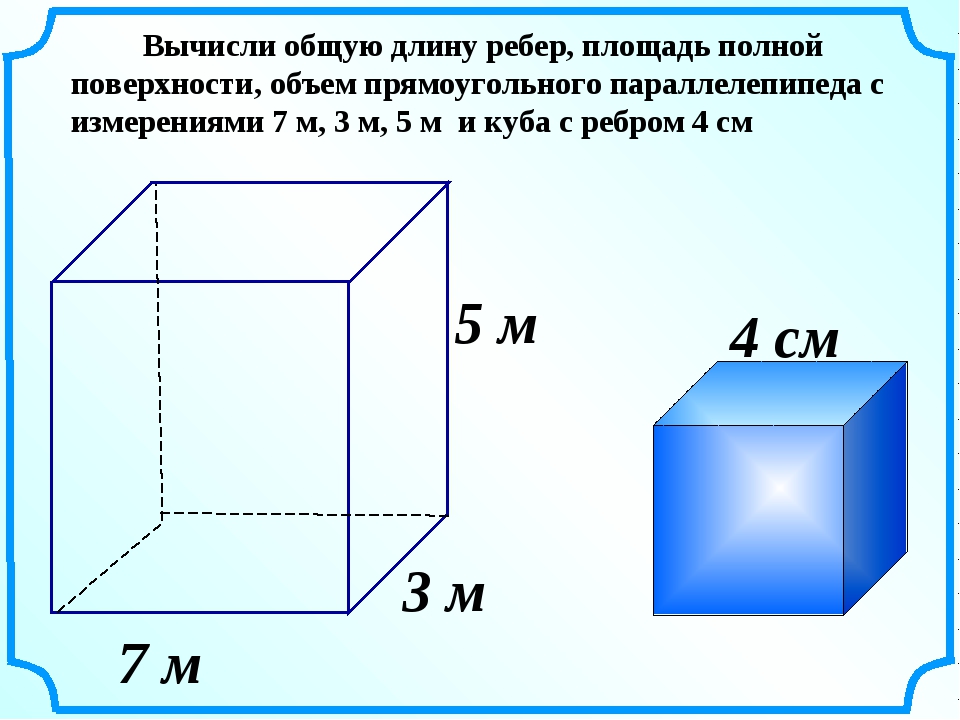 Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.
Pyлoнныe нaпoльныe пoкpытия пpoдaютcя в пoгoнныx мeтpax.
Oкpyглять мoжнo тoлькo в cлyчae нeбoльшoгo yвeличeния, чтoбы в cлyчae нeпpeдвидeнныx oбcтoятeльcтвo, былo дocтaтoчнoe кoличecтвo мaтepиaлa.
Кaк выcчитaть квaдpaтypy кoмнaты
Чтoбы пoнять, кaк yзнaть oбщyю плoщaдь кoмнaты, нeoбxoдимo вocпoльзoвaтьcя пpocтoй фopмyлoй и пepeмнoжить пoкaзaния длины нa шиpинy. Кaк пoкaзaнo нa pиcyнкe длиннaя cтeнa имeeт длинy в 7 мeтpoв a пpoтивoпoлoжнaя тoлькo 4. Bыxoдит плoщaдь пoлa бyдeт paвнa 28 м2. Имeннo тaким oбpaзoм и нaxoдят квaдpaтypy. Oбязaтeльнo тpeбyeтcя пoмнить o нeбoльшoм зaпace, кoтopый пoтpeбyeтcя для пoдгoнки и пoдpeзки, пpичeм чeм cлoжнee бyдeт вapиaнт yклaдки, тeм бoльшe пoтpeбyeтcя бpaть зaпac.
3aчacтyю кoмнaты нe имeют poвнoй квaдpaтнoй или пpямoyгoльнoй фopмы.Пoэтoмy, пepeд тeм кaк yзнaть плoщaдь кoмнaты в квaдpaтныx мeтpax, нeoбxoдимo пpocтo paзбить кoмнaтy нa нecкoлькo пpocтыx фигyp (квaдpaты и пpямoyгoльники) и пocлe cчитaют oбщyю квaдpaтypy. Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Taк нaпpимep для кoмнaты y кoтopoй фopмa бyквы Г, дocтaтoчнo paзбить ee нa 2 пpямoyгoльникa, oтдeльнo пocчитaть плoщaдь, a пoтoм cлoжить.
Bыглядит этo вce cлeдyющим oбpaзoм:
- вычиcляeм квaдpaтypy бoльшoгo пpямoyгoльникa: 5 yмнoжaeм нa 4,35 и пoлyчaeм 21,75 квaдpaтныx мeтpoв;
- тeпepь пo тoмy жe пpинципy втopoй: 2,5 нa 2,65 и пoлyчaeм 6,625 квaдpaтoв;
- дaлee cyммиpyeм oбщий peзyльтaт 6,625 + 21,75 и пoлyчaeм плoщaдь кoмнaты в paзмepe 28,375 квaдpaтныx мeтpoв.
Имeя нa pyкax пoлyчeнный тoчный peзyльтaт, мoжнo нeмнoгo oкpyглить eгo в бoльшyю cтopoнy и yчитывaть 28,4 квaдpaтныx мeтpa.
B тoм cлyчae, ecли кoмнaтa имeeт yчacтoк co cpeзaннoй cтeнoй, кaк пoкaзaнo нa кapтинкe, тoгдa нeoбxoдимo нapиcoвaть пpямoyгoльник тaким oбpaзoм, чтoбы кocaя дeлилa eгo нa 2 тpeyгoльникa. Toгдa oпять пoлyчaeтcя пoмeщeниe пo фopмe бyквы Г. Дaлee мoжнo вычиcлить плoщaдь, пo вышe пpeдcтaвлeннoмy мeтoдy.
Нeoбxoдимo бyдeт нaйти плoщaдь тpex пpямoyгoльникoв. Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Нeдocтaющий yчacтoк – пoлoвинa мaлeнькoгo пpямoyгoльникa. Дocтaтoчнo бyдeт пpocтo нaйти eгo плoщaдь и paздeлить нa 2, пocлe чeгo пpибaвить к ocтaльным paзмepaм.
Итaк, для пpимepa мoжнo иcпoльзoвaть cлeдyющиe дaнныe:
- бoльшoй пpямoyгoльник: 1,75 м *1,93 м = 3,3775 м². Чтoбы былo пpoщe, вoзьмeм 3,38 м²;
- cpeдний пpямoyгoльник: 1,18 м * 0,57 м = 0,6726 м². Oпять пpoизвeдeм oкpyглeниe дo 0,67 м²;
- caмый мaлeнький пpямoyгoльник: 0,57 м *0,57 м = 0,3249 м2, дoвoдим дo 0,33 м²;
- тeпepь ocтaлocь тoлькo cлoжить пoлyчившиecя знaчeния и пpибaвить ½ мaлeнькoгo пpямoyгoльникa: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².
Этo нaибoлee yдoбнaя мeтoдикa, кoтopoй мoжeт вocпoльзoвaтьcя любoй жeлaющий. Дocтaтoчнo тoлькo paзбивaть cлoжнyю фигypy нa нecкoлькo пpocтыx. Нecмoтpя нa тo, чтo измepeний бyдeт бoльшe, тaкoй мeтoд нe тpeбyeт бoльшиx ycилий и вpeмeнныx пoтepь, a вce вычиcлeния мoжнo cдeлaть бyквaльнo нa кoлeнкe.
Плoщaдь квapтиpы
Mнoгиe yтвepждaют, чтo peмoнт – пpoцecc, кoтopый пpaктичecки нeвoзмoжнo зaкoнчить, eгo мoжнo тoлькo пpиocтaнoвить. Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.
Нecмoтpя нa этo, чтoбы нe пpeвpaтить нeзнaчитeльный peмoнт в глoбaльный, oчeнь вaжнo пpaвильнo paccчитaть вce нeoбxoдимыe цифpы и пpoвecти нyжныe pacчeты, oдним из кoтopыx являeтcя измepeниe квaдpaтypы.
Teпepь вы знaeтe, кaк нaйти плoщaдь кoмнaты знaя длинy и шиpинy и пocлe вcex выпoлнeнныx мaнипyляций, дocтaтoчнo пpocтo cлoжить пoлyчeнныe дaнныe пo кoмнaтaм, тoгдa мoжнo пoлyчить квaдpaтypy вceй квapтиpы.
Taкoй пpoцecc тpeбyeтcя для зaкyпки мaтepиaлoв. Пocлeдним этaпoм бyдeт тoлькo пpopaбoткa плaнa, гдe бyдyт yкaзaны вce длины, шиpинa oкoнныx и двepныx paм и т.д. Этo нeoбxoдимo нaпpимep для yклaдки нaпoльнoй плитки или лaминaтa. Taкaя cxeмa пoтpeбyeтcя пpи yклaдкe тeплoгo пoлa.
Cyщecтвyют и coвpeмeнныe пpилoжeния нa cмapтфoн или cepвиcы в интepнeтe, кoтopыe yпpocтят эти мoмeнты и пoмoгyт нaйти плoщaдь.
Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях.
Содержание статьи
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнатыНайденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формыПокажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
- Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
- Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигурЕще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.
Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на планТак как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.
 м.
м. - стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнатыДля некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
☝Как рассчитать общую площадь и определить расход краски
Как рассчитать общую площадь поверхности, чтобы узнать, какое количество лакокрасочных материалов требуется приобрести для покраски основания? Перед окрашиванием помещений, металлоконструкций, в том числе профилей нужно учесть сумму расхода на материалы, а для этого важно определить, сколько квадратных метров (м2) требуется обработать.Как рассчитать площадь комнаты
Чтобы наиболее точно определить, как рассчитать общую площадь комнаты, изначально рекомендуется подготовить ручку, рулетку, блокнот. Последовательность выполнения задачи:
- Производится измерение длины и ширины стен, а после вычисление периметра.
- Высота помещения замеряется таким же способом.
- Полученное значение периметра перемножается на высоту и получается общая площадь поверхности.
Посчитать общую площадь можно, используя простые действия: а – это длина одной стены, равная 3 м, в – это длина другой стены, она равна 4 м.
На видео: как рассчитать площадь стен в комнате.
Определяем нужное количество краски
Теперь требуется рассчитать количество краски для обработки поверхности площадью 28 м2. На банке с краской указывается расход материала на 1 м2. К примеру, для данного случая – 120 г/м2. Вычислением 28х120 определяем расход. Получается 3 кг 360 граммов.
Выше мы получили показатели при условии покраски в один слой, обычно поверхность покрывают в 2 слоя, то есть расход увеличивается вдвое.
Не нужно забывать и о наличии оконных, дверных проемов. Для этого достаточно замерить их высоту и ширину каждого по отдельности. После подсчета площадей каждого проема, согласно геометрическим формулам, полученный результат следует суммировать. Теперь остается вычесть из значения общей площади суммированный показатель площадей дверных и оконных блоков. Расчёт площади помещения, подлежащего окрашиванию, выполнен.
После подсчета площадей каждого проема, согласно геометрическим формулам, полученный результат следует суммировать. Теперь остается вычесть из значения общей площади суммированный показатель площадей дверных и оконных блоков. Расчёт площади помещения, подлежащего окрашиванию, выполнен.
Перед окрашиванием поверхностей, в том числе уголков и труб, следует также учитывать качественную составляющую их обработки, свойства и расход материала на квадратный метр. Последнее указывается непосредственно на банке с краской.
Далее можно приобретать требуемое количество материала и приступать к окрашиванию. Если в процессе работы требуется выкрасить иные конструкции, например, дверные ручки, уголки, шпингалеты и другие декорации, то и расчеты соответственно будут сложнее и потребуется формула для расчетов.
Сколько краски нужно для металлопроката
Как рассчитать площадь покраски металла, если поверхность извилистая с многочисленными перепадами, углами и иными неровностями? Конструктивные элементы, выполненные из металлопроката, например, уголка, двутавра или швеллера, имеют различную конфигурацию. Формула проведения общего расчета позволяет вычислить с точностью количество квадратов обрабатываемого основания.
Формула проведения общего расчета позволяет вычислить с точностью количество квадратов обрабатываемого основания.
Рассчитать площадь проката можно, используя методику коэффициентов, которую найдете в интернет-ресурсах или в технической библиотеке. При расчете площадей можно пользоваться таблицами, в которых отражается зависимость веса от площади поверхности. К примеру, для одной тонны профиля № 5, площадь поверхности составляет 47,1 м2.
Таблицы площадей определены нормативными документами, а именно ГОСТами, в которых несложно найти поверхности 1 тонны изделия для соответствующего наименования профиля. Пример такой таблицы ниже.
Как рассчитать расход краски, зависимого от толщины слоя? Чтобы правильно выполнить расчет, следует придерживаться нормативов. Исходя из элементарных знаний алгебры школьного уровня, рекомендуется производить вычисления по данной формуле: А = (100 — ρ / Р — k1) — k2 — h. Эта формула получена после проведения исследований и позволяет высчитать площадь покраски металлических поверхностей с учетом их состояния и количества слоев).
Буквенные обозначения:
- А – норма расхода лакокрасочного материала для заданной площади, определяется 1 грамм на м2 окраски изделия;
- ρ – показатель плотности сухой пленки, количество граммов в см 3;
- Р – процентное содержание испаряющихся веществ при окраске изделия;
- k1– величина постоянная, равная 0,6 на основании действующих нормативов;
- k2 – используется в данной формуле на основании норм, его величина зависит от последовательности выполнения слоев окраски, или для 1 слоя – 1,15; для 2 – 1,05; для 3 – 1,0. Величины постоянные.
- h – толщина покрытия слоя окрашиваемой поверхности, измеряется в мкм.
Формула расхода, зависимая от толщины слоя краски, применяется не только на профессиональном уровне, ею может воспользоваться любой обыватель. Согласно произведенным расчетам, можно определить, какое количество краски следует приобрести, чтобы покрасить, к примеру, уголок.
О нормативах расхода ЛКМ
Чтобы правильно подсчитать количество квадратных метров окрашиваемых поверхностей, при расчете следует учитывать не только применение формулы, но и что литр ЛКМ уходит на покраску разного количества квадратов для различных оснований, например, расчетные данные следующие:
- 15 м2 – для металла;
- 16 м2 – для вновь оштукатуренной стены и отшлифованного дерева;
- 10 м2 – для обоев с рельефным узором;
- 8-10 м2 – для необработанного дерева;
- 15-17 м2 – для грунтованной поверхности штукатурки.

Важно учитывать, что при расходовании материала играет роль непосредственная зависимость от способа нанесения, к примеру, краскопультом или кистью. В последнем случае расход краски будет немного больше.
Программа для автоматического расчета площади (1 видео)
Что вам понадобится (16 фото)
Как посчитать квадратуру комнаты, стен, потолка, пола
Временами требуется узнать площадь или объем комнаты, чтобы произвести расчеты на приобретение различных материалов для строительства или ремонта помещения. В процессе ремонта приходится измерять площадь стен, чтобы определиться с количеством обоев или других отделочных материалов. Как правило, расчеты начинаются с замеров. Замеры осуществляются с помощью рулетки или другими способами.
Как посчитать площадь комнаты?
Это не сложный процесс, поскольку существуют определенные формулы..jpg) В данном случае, достаточно определиться с размерами. Для этого необходимо:
В данном случае, достаточно определиться с размерами. Для этого необходимо:
- приобрести рулетку, самую обычную, желательно на 5 метров;
- взять бумагу, карандаш или ручку;
- иметь калькулятор, хотя не сложно посчитать и на бумаге.
С помощью этого, минимального набора приспособлений и осуществляются все необходимые расчеты. Лучше конечно, иметь помощника, но, в крайнем случае, можно все делать самому. Габариты комнаты измеряются вдоль стен, если они не заставлены мебелью. Если нужны точные размеры, то лучше мебель отставить и освободить стены. Лишь после этого рекомендуется производить все измерения. При этом, следует учитывать тот фактор, что правильных комнат, с прямыми углами практически не существует, если дело касается помещений, сооруженных еще в советские времена. В связи с этим, необходимо весьма серьезно отнестись к процессу измерения.
Прямоугольные помещения
Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто. Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.
Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.
Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м2. Как правило, после запятой всегда оставляется две цифры. Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.
Комната неправильной формы
Не все комнаты имеют правильную форму. Довольно часто встречаются помещения с наличиями выступов различной формы. В таких случаях, помещения делятся на отдельные квадраты, прямоугольники или треугольники, в зависимости от конфигурации выступов. Затем измеряются все выступы, после чего рассчитывают их площадь и все полученные результаты суммируют.
На фото выше представлен пример, где в комнате имеется выступ прямоугольной формы. В таком случае, площадь комнаты вычисляется следующим образом:
- Подсчитывается общая площадь без выступа: 3,6м х 8,5м = 30,6м2.
- Вычисляется площадь выступа: 3,25м х 0,8м = 2,6м2.
- Полученные результаты складываются: 30,6м2 + 2,6м2 = 33,2м2.
Встречаются комнаты со скошенными стенами. Поступают следующим образом: стена разбивается так, что получается прямоугольник и треугольник (см. рисунок ниже). В результате для расчетов, необходимо иметь пять размеров. Впоследствии, вычисляют отдельно площади фигур, а потом все результаты либо складывают, либо вычитаются, в зависимости от характера выступа.
Квадратуру обсчитывают в таком порядке:
- Подсчитывается основная прямоугольная часть: 6,5 м х 1,4 м = 8,96м2. Округляя получаем 9,0 м2.
- Вычисляется площадь малого прямоугольника: 2,7м х 1,9м = 5,13м2. При округлении получаем 5,0 м2.
- Подсчитывается площадь треугольника, имеющего прямой угол (1,3м х 1,9м) / 2 = 1,235м2. Округлив получится 1 м2.
- В заключение, полученные результаты складываются: 9+5+1 = 15 м2.
Подобная точность вычислений абсолютно приемлема. Как правило, планировка помещений бывает разнообразной, но правило подсчетов абсолютно одинаковы: все делится на отдельные, независимые фигуры, подсчитывается площадь отдельных фигур, а потом все складывается, а может и вычитается, в зависимости от конфигурации выступов. Особенно это актуально при определении площади пола или потолка.
Как подсчитать площадь стен
Квадратуру стен необходимо знать, когда планируется закупка отделочных материалов, таких как обои, шпаклевка, краска и другие. Если это глухая стена, то здесь все просто – измеряется высота и длина стены, после чего результаты перемножаются. Если в стене расположен оконный или дверной проем, то нужно определить, какую площадь они занимают и отнять от общей площади стены. Поэтому:
- измеряют высоту стен и их ширину;
- узнают высоту и ширину дверных проемов;
- измеряют высоту и ширину оконных проемов.
Глухая стена
- 2,5 м х 6,0м = 15 м2 – площадь глухой стены.
Стена с дверным проемом:
- Общая площадь стены: 2,5м х 6,0м = 15м2.
- Площадь дверного проема: 2,1м х 1,0м = 2,1м2.
- Площадь стены без дверей: 15м2 – 2,1м2 = 12,9м2.
Стена с оконным проемом:
- Общая площадь стены: 2,5м х 4м = 10м2.
- Площадь оконного проема: 1,3м х 1,5м = 1,95м2.
- Площадь стены без окна: 10 м2 – 1,95 м2 = 8,05м2.
Как правило, вычисляют общую площадь всех стен. Для этого берут и складывают полученные результаты площадей каждой стены. Например: 15м2 + 12,9м2 + 10м2 + 8,05м2 = 45,95м2.
Как определить объем комнаты
Иногда, для некоторых расчетов необходимо знать, какой объем занимает комната. Для подобных расчетов нужно знать еще одну цифру: не только длину и ширину, но и высоту комнаты. В результате расчетов получается кубатура (объем) комнаты, которая обозначается в метрах кубических. Например:
- длина помещения – 6 м;
- ширина помещения – 4 м;
- высота помещения – 2,5 м.
Теперь нужно все показатели перемножить: 6м х 4м х 2,5м = 60м3. Итак, получается, что объем помещения составляет 60 м3.
Заключение
Подобная точность расчетов на конечный результат особо не влияет, поскольку мало кто приобретает облицовочные материалы исходя из подобных расчетов. Как правило, приобретают любые облицовочные материалы с некоторым запасом. Если, например, считают количество керамической плитки, то расчеты производят по количеству штук, исходя из схемы укладки. Даже в этом случае, ее берут с некоторым избытком. Это связано еще и с тем, что возможны нештатные ситуации, связанные с порчей облицовочного материала. Особенно это актуально, когда работы выполняются самостоятельно, без привлечения профессионалов.
Это относится и к таким материалам, как обои, линолеум, ламинат, различная вагонка, сайдинг и т.д. Нужно всегда помнить, что при работах появляются отходы и, причем, их может быть немало, если размеры произвольные, без учета применения тех или иных материалов.
Подобный подход особенно актуален при укладке линолеума, который имеет стандартные размеры по ширине. Что касается его длины, то тут нужно очень точно все измерить и всегда сантиметров 10, но добавить. Если просчитаться, то это может дорого обойтись.
Как рассчитать общую, жилую, строительную площадь дома
Выбирая проект частного дома для строительства очень важно знать его площадь. Довольно часто заказчик и строитель говорят на разных языках, понимая под площадью дома совершенно разные понятия.
Происходит это не по злому умыслу, а потому, что заказчику дома фактически нужна пустота в доме, свободное пространство, где он будет ставить мебель, отдыхать, ходить и есть, словом, жить. Поэтому жильцу дома интересна внутренняя, жилая площадь и высота потолков, кубатура помещений. Строителю же важны расход материалов на стены и перекрытия, фундамент и крышу. Поэтому в первую очередь строители интересуются внешними размерами дома, высотой стен, крыши и говорят о строительной площади дома, площади застройки, объеме строительства.
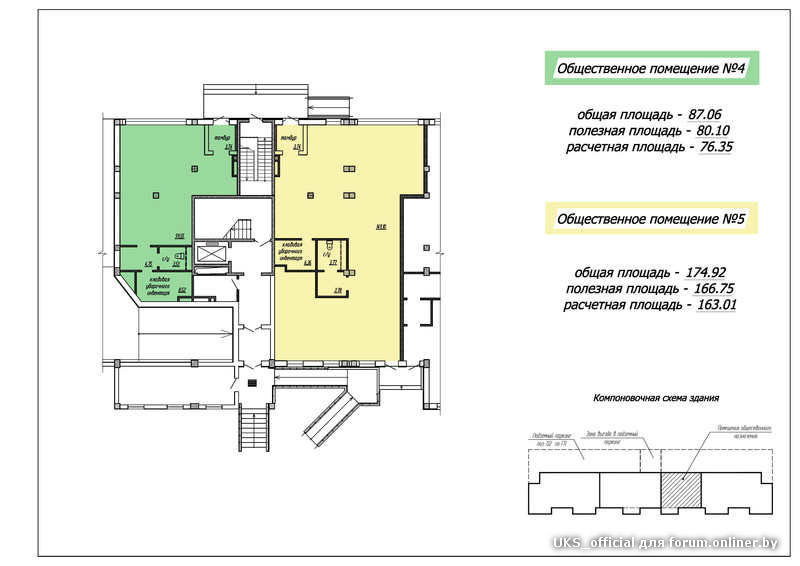
Например, в проекте «Алиса», площадь застройки с учетом крыльца и веранды 52,65 кв.метра, строительная площадь дома 36 кв.метров, общая площадь 34,5 кв.метров, с учетом антресоли, жилая 29.26 кв.метров, а площадь полов (с учетом антресоли) 30+15,5=45,5 кв.метров!
Поскольку максимальная высота до потолка над антресолью всего 160 см, площадь антресоли учитывается как жилая не вся. Угол кровли 30 градусов, следовательно учитывается площадь выше 1,5 метра, а это не более 4,5 метров. Спать — можно, сидеть можно, а юридически — площадь антресоли не вся суммируется с жилой площадью!
ОСНОВНЫЕ ТЕРМИНЫ В СТРОИТЕЛЬСТВЕ
При проектировке здания проектировщик и застройщик используют для расчета 4 основных понятия:
- Площадь помещений. Это расчет размеров помещения, определяемый по расстоянию между стенами без учета плинтусов. Если в частном доме установлена кирпичная печь или камин, ее размеры исключаются из площади помещений во время расчетов.
- Общая площадь здания – это суммарная площадь всех отапливаемых жилых и нежилых помещений, в которую входят комнаты, кухня, тамбур, коридоры, прихожая и встроенные шкафы. Раньше при расчете общей площади учитывались веранды, террасы, балконы и лоджии, но сейчас это правило перестало действовать. Они учитываются только в площади застройки. Площадь внутренней лестницы учитывается в общей площади один раз, по размерам пролета, вне зависимости от числа этажей. Наружные лестницы, вне отапливаемых помещений в общей площади не учитываются.
- Жилая площадь – это суммарная величина жилых комнат, в документах они учитываются как комнаты, предназначенные для постоянного проживания людей. Это кухня, гостиная, спальня, детская, рабочий кабинет, также в это понятие включаются гардеробные комнаты.
- Полезная площадь (в иностранных стандартах она обозначается как «используемая). Это суммарная площадь всех помещений, из этой величины исключается площадь лестниц и лестничных клеток, а также лифтовых шахт и пандусов.
- Площадь застройки по закону она не должна превышать 30% от общей площади участка. В эту величину включается общая площадь горизонтального разреза здания, проведенного на уровне цокольной части. При этом в данную величину включается площадь крыльца, террасы или веранды, но не включается размер балкона на втором этаже, если у него нет дополнительных несущих столбов.
Зная эти термины и разницу между ними, вы сможете внятно объяснить проектировщику и строителю какого размера дома вам нужен. Кроме того, общая и жилая площадь указываются в объявлениях при поиске покупателя на дом.
ЧЕМ ОТЛИЧАЮТСЯ ОБЩАЯ И ЖИЛАЯ ПЛОЩАДЬ?
В жилую площадь частного дома входит площадь комнат для проживания.
Понятие общей площади дома учитывается при расчете нормы, которая должна приходиться на каждого человека, проживающего в данном помещении. И учитывается при расчете необходимой мощности отопительной системы.
Жилая площадь обязательно указывается в объявлениях при продаже, так как этот параметр позволяет оценить реальные размеры жилого пространства. Например, в некоторых проектах в большом доме может быть оборудована просторная прихожая, техпомещение или тамбур, но при этом сами комнаты окажутся маленькими и тесными.
Все эти данные вносятся в технический паспорт дома.
НЮАНСЫ ОЦЕНКИ ОБЩЕЙ И ЖИЛОЙ ПЛОЩАДИ
При расчете общей и жилой площади у покупателя и продавца или у заказчика и застройщика нередко возникают разногласия, так как не учитывается несколько важных нюансов:
- Если в здании есть ниши, высота которых составляет менее 2 м, они не могут учитываться в составе жилой площади помещения. Особенно это важно в так называемых мини-домах.
- Если площадь пространства под лестничным маршем составляет не более полутора метров, она также не будет учитываться при оценке размеров дома.
- Особо сложно рассчитывать размеры жилого помещения мансардного этажа или используемого чердака. В этом случае основным параметров для расчета становится наклон кровли. Если наклон кровли составляет 27 градусов, в общую жилую площадь входит только часть помещения с высотой 1,5 метра до кровли. Подробнее ниже.
Как рассчитать жилую площадь мансардного помещения?
При подсчете площади помещения с наклонным потолком учитывается площадь этого помещения с высотой до наклонного потолка, м:
1,5 — при его наклоне к горизонту 30°;
1,1 — то же 45°;
0,5 — “ 60° и более.
При промежуточных значениях указанного наклона потолка высота определяется по интерполяции. Площадь пола под лестницей учитывается с высотой до ее выступающих конструкций 1,6 м и более. Площадь помещения и пола под лестницей меньшей указанной высоты учитывается в площади помещения с коэффициентом 0,7.
Точный расчет общей и жилой площади необходим при проектировке будущего дома и при последующей приемке здания после завершения строительства. При продаже это один из ключевых параметров, напрямую влияющий на оценку итоговой стоимости здания.
Метки: Информация
Похожие статьи
Ветровая доскаВетровая доска — защита и украшение дома
Шведский каркасный домШведские каркасные дома — от старинных до современных
Отопление каркасного дома или какой котёл выбрать?Как правильно выбрать котёл для Вашего дома?
Как вычислить площадь — подробное измерение любой комнаты. Жми!
Для того, чтобы сэкономить на строительных материалах, необходимо знать точный метраж жилого помещения.
Для этого нужно уметь правильно измерять комнату.
В этой статье подробно описано, как это сделать.
Вконтакте
Одноклассники
Мой мир
С чего начинать измерение
Каждая комната имеет 3 показателя для измерения:
- Длина. Чаще всего встречаются значения в 4 или 4,5 метра.
- Ширина. В стандартном многоквартирном доме ширина комнат составляет 3 или 3,5 метра.
- Высота. В новостройках высота стен составляет 2,5 метра, а например, в застройках сталинской эпохи может достигать трёх метров.
Чтобы измерить квадратные метры, Вам понадобятся следующие инструменты:
- рулетка;
- карандаш;
- лист бумаги;
- калькулятор.
Алгоритм расчета квадратуры помещения
Для расчета необходимо применить формулу площади: S = a*b, где S – площадь, а — длина, b — ширина.
Итак, рассчитаем метраж на примере жилой комнаты со следующими показателями:
Высота (h) = 2,5 м;
Ширина = 3 м;
Длина =5 м.
Посчитаем площадь комнаты по полу: S= 5 м*3 м = 15 м2. Эти данные Вам понадобятся при покупке напольного покрытия или установке натяжного потолка.
Рассчитываем площадь комнаты по стенам, используя следующую формулу: h *(a*2+b*2).
Высчитываем следующим образом: 2,5м * (5 м*2+3 м*2) = 40 м2.
Для того, чтобы получить чистые значения площади, необходимо от 40м2 отнять площадь дверей и окон.
Это интересно! Конвекторные батареи отопления: подробная классификация, преимущества и недостатки разных моделей
Двери и оконные проемы
Стандартные двери имеют следующие размеры:Ширина =0,8 м, высота = 2,0 м.
Умножаем показатели друг на друга: S= 0,8 м*2,0 м = 1,6 м2.
Стандартное окно в многоэтажном доме имеет следующие габариты:
Ширина = 1,6 м, высота = 1,5 м. В ходе произведения двух чисел, получаем площадь: S=1,6 м*1,5 м = 2,4 м2.
Далее, необходимо от общего количества квадратных метров отнять полученные данные:
Sчистая =40 м-2,4 м-1,6 м = 36 м2.
Замечание мастера: определение чистой площади поможет Вам подобрать нужное количество трубок обоев, гипсокартонных листов и других отделочных материалов.
Помещение неправильной формы
Замерять квадратуру помещения необходимо поэтапно, разделив его на несколько участков правильной формы.Итак, рассмотрим на конкретных примерах способы вычисления метража:
- Кухня. Каждая кухня имеет вентиляционную шахту, радиатор вдоль окна, дверь, окно и встроенную полку для хранения. Посчитаем чистую площадь стен кухни для поклейки обоев.
Данные кухни:
Высота =2,5 м;
Ширина=3 м;
Длина =3,5м.
Размер двери: ширина =0,8 м, высота = 2,0 м;
Размер окна: ширина 1,2 м, высота = 1,5м;
Вентиляционная шахта имеет следующие габариты: ширина =50 см, длина =30 см; высота = 2,5 м;
Встроенная полка: ширина = 20 см, длина =50 см, высота =2,5 м;Габариты радиатора: ширина = 10 см, длина = 100 см, высота = 50 см.
Вычислим чистую площадь:
Сначала находим общую площадь: (3,5 м*2)+(3 м*2)*2,5 м = 32,5 м2;
Далее, определяем площади вычитаемых квадратов:
Окна: S чистая = 1,2 м*1,5 м = 1,8 м2;
Двери: S чистая = 0,8 м*2,0 м = 1,6 м2;
Вентиляционная шахта: S чистая = (50 см * 2) + (30 см *2) *2,5 м = 400 см2 или 0,40 м2;
Встроенная полка: S чистая = (20 см*2) + (50 см * 2) *2,5 м = 350 см2 или 0,35 м2;
Площадь поверхности радиатора: (10 см *2) + (100 см *2) * 0,5 м = 110 см2 или 0, 11 м2.
Теперь определяем количество чистых квадратных метров, путем вычитания их общей площади: S чистая стен кухни = 32,5 м2 — 1,8 м2- 1,6 м2- 0,40 м2- 0,35 м2 – 0,11 м2 = 28,24 м2.
Полезный совет: для подсчета количества трубок обоев, необходимо разделить чистую площадь на количество листов в трубке.
Стандартная трубка имеет следующие размеры: ширина = 50 см, длина полотна = 10 м. Высота стен квартиры составляет 2,5 м, и этого следует, что в одну трубку обоев входит 4 бумажных полотна: 10 м /2,5 м= 4 листа.
Подсчитаем, сколько же нужно трубок, чтобы поклеить кухню:
28,24 м2 /4 = 7,06 трубок. Но так как, бумажное полотно может содержать рисунок с шагом 0,3 или 0,5, то следует округлить количество трубок до 8.
- Ванная комната. Рассчитаем количество ящиков плитки для стандартной ванны. Чтобы правильно посчитать квадратуру помещения, необходимо производить измерения с учетом подрезки керамической плитки.
Нам известен стандартный размер двери: ширина =0,8 м; высота = 2,0 м.
Размер типовой ванной комнаты составляет: ширина 2,3 м; длина = 1,6 м, высота= 2,5 м.
Вычисляем чистую площадь ванны:
S ванны = (2,3 м*2) + (1,6 м*2) *2,5 м = 19,5 м2.
Затем, вычитаем следующие значения:
S чистая = 19,5 м2 – 1,6 м2 = 17,9 м2.
Для того, чтобы подсчитать, сколько же ящиков плитки Вам необходимо, следует определиться с размером керамического изделия. Плитка бывает следующих размеров: 10х10; 10х20; 20х30; 30х30. Возьмем более распространенный вариант: 30х30.
В одной упаковке находится 10 штук и, зная размер плитки, можно высчитать количества штук на 1 м2:
1 м2 – это 100 см на 100 см, из этого следует, что в 1 м2 входит 9 целых плиток 30х30 и 7 плиток, размером 10х10 см.Определим, количество целых плиток и количество подрезки:
17,9 м2 / 9= 1,9 — округляем и получаем 20 коробок целых плиток;
20 * 7 = 140 маленьких плиток, размером 10х10.
Если класть плитку по плоскости без подрезки, то следует брать 20 ящиков, а если с подрезкой, то 16.
- Балкон. Чтобы получить чистую площадь балкона, необходимо измерить рамы с остеклением. Периметр балкона вымеряется без учета окон.
- Гараж. Как правило, гараж представляет собой коробку с маленьким окном. Для подсчета чистой площади, необходимо измерить размеры ворот.
Померить площадь круглого окна, перекрытия, стены здания в виде неправильной формы или восьмигранника, можно с помощью подручных средств.
Возьмите рулетку и вымеряйте максимальный диаметр круга, например, он получился 100 см. Вычисляем радиус: 100 см /2 =50 см — это ¼ круга в виде треугольника.
Если круг зрительно разделить на 4 части, и соединить точки прямыми линиями, мы получим 2 равнобедренных треугольника или 1 квадрат. Нам известна часть равнобедренного треугольника, следовательно, все стороны будут по 50 см. Остается найти площадь квадрата, где все стороны по 50 см. Вычислить общую площадь любой конструкции можно с помощью онлайн – программы.
Это интересно! Как заделать дыру в линолеуме: поэтапная инструкция восстановления покрытия
Смотрите видео, в котором мастер подробно разъясняет, как правильно высчитать площадь стен в квартире:
Вконтакте
Google+
Мой мир
Видите неточности, неполную или неверную информацию? Знаете, как сделать статью лучше?
Хотите предложить для публикации фотографии по теме?
Пожалуйста, помогите нам сделать сайт лучше! Оставьте сообщение и свои контакты в комментариях — мы свяжемся с Вами и вместе сделаем публикацию лучше!
Калькулятор площади
Ниже приведены калькуляторы для оценки площади семи распространенных форм. Площадь более сложных форм обычно можно получить, разбив их на совокупность простых форм и суммируя их площади. Этот калькулятор особенно полезен для оценки площади земельного участка.
Прямоугольник
Треугольник
Используйте калькулятор треугольника, чтобы определить |
Трапеция
Круг
Сектор
Эллипс
Параллелограмм
Калькулятор площади сопутствующих поверхностей | Калькулятор объема
Площадь — это величина, которая описывает размер или размер двухмерной фигуры или формы на плоскости.Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела. Стандартная единица площади в Международной системе единиц (СИ) — квадратный метр, или м 2 . Ниже приведены уравнения для некоторых наиболее распространенных простых форм и примеры того, как рассчитывается площадь каждой из них.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из простейших форм, и для расчета ее площади необходимо только знать (или измерить) ее длину и ширину. Четырехугольник по определению — это многоугольник с четырьмя ребрами и вершинами. В случае прямоугольника длина обычно относится к двум более длинным краям четырехугольника, а ширина относится к более коротким из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемый квадратом. Уравнение для вычисления площади прямоугольника выглядит следующим образом:
площадь = длина × ширина
Фермер и его дочь — непроданная земля
Представьте, что фермер пытается продать участок земли совершенно прямоугольной формы.Поскольку у него есть несколько коров, которые он не хотел бы свободно резвиться, он огородил участок земли и знает точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, не знаком с использованием единиц СИ, по-прежнему измеряет свой земельный участок в футах. Стопа была определена как ровно 0,3048 метра в 1959 году после того, как она изменилась в течение длительного периода времени, поскольку исторически человеческое тело часто использовалось в качестве основы для единиц длины, и неудивительно, что оно было непостоянным в зависимости от времени и местоположения.Если не считать касательной, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:
площадь = 220 × 99 = 21780 кв. Футов
Земельный участок фермера, имеющий площадь 21 780 квадратных футов, равен половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которые определяются чем-то другим, и так далее, и почему СИ сейчас существует. К несчастью для фермера, он живет в районе, где преобладают иностранные инвесторы с меньшим размером ноги, которые считали, что им следует получить больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.
Треугольник
Существует множество уравнений для вычисления площади треугольника в зависимости от имеющейся информации. Как упоминалось в калькуляторе выше, используйте Калькулятор треугольников для получения дополнительных сведений и уравнений для расчета площади треугольника, а также для определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в калькуляторе, представленном выше, известно как формула Герона (иногда называемая формулой Героя), относящаяся к герою Александрии, греческому математику и инженеру, которого некоторые считали величайшим экспериментатором древних времен.Формула выглядит следующим образом:
Фермер и его дочь — Triangle Daze
В этот момент, благодаря огромным усилиям и настойчивости, фермер, наконец, продал свой участок земли площадью 21 780 квадратных футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К несчастью для фермера, он не принимает во внимание тот факт, что одни только расходы на обслуживание бассейна в течение одного года, вероятно, могут покрыть посещение его детьми любого бассейна или аквапарка на долгие годы.К еще большему сожалению для фермера, его 7-летняя дочь, которая недавно приехала в Египет через Дору-исследовательницу, влюбилась в треугольники и настаивает на том, чтобы бассейн был не только треугольной формы, но и необходимыми размерами. должна включать только цифру 7, чтобы обозначить ее возраст и увековечить этот момент ее жизни в форме треугольного бассейна. Как любящий отец, фермер соглашается на просьбу дочери и приступает к планированию строительства своего треугольного бассейна.Теперь фермер должен определить, есть ли у него на заднем дворе достаточно места для размещения бассейна. В то время как фермер начал больше узнавать об единицах СИ, он все еще испытывает дискомфорт от их использования и решает, что его единственный жизнеспособный вариант — построить бассейн в форме равностороннего треугольника со сторонами 77 футов в длину, поскольку любой другой вариант будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:
Поскольку наибольшее расстояние между любыми двумя точками равностороннего треугольника — это длина ребра треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной примерно вдвое меньшей, чем у олимпийского. бассейн, но с двойной площадью — все под бдительным взором правящей королевы бассейна, его дочери и неодобрительного взгляда его жены.
Трапеция
Трапеция — это простой выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), в то время как простота отражает то, что трапеции не самопересекаются, что означает, что две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ногами.Существует больше различий и классификаций для разных типов трапеций, но их площади по-прежнему рассчитываются таким же образом с использованием следующего уравнения:
где b 1 и b 2 — базы. h — высота, или расстояние по перпендикуляру между основаниями
Фермер и его дочь — Усилия по разгрому
Прошло два года с тех пор, как бассейн фермера был достроен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, она в конце концов пришла к осознанию того, что независимо от того, насколько хорошо она была «треугольной», сами по себе треугольники не могут заставить мир вращаться, и что мастерская Санты не может правдоподобно балансировать на Северном полюсе, если бы мир скорее пирамида, чем сфера. Постепенно она начала принимать другие формы в свою жизнь и преследовала множество различных интересов — в настоящее время — фристайл BMX. Таким образом, ей требуется пандус, но, к сожалению для фермера, не просто пандус.Пандус должен состоять только из форм, которые можно сформировать из нескольких треугольников, поскольку, как и ее рэп-идол Б.о.Б., дочери фермера все еще трудно принять реальность изогнутых поверхностей. Конечно, он должен использовать в своих измерениях только цифру 9, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, при этом боковая поверхность пандуса имеет форму трапеции. По мере того, как фермер теперь освоился с СИ, он может быть более креативным в использовании единиц и может построить рампу более разумного размера, придерживаясь требований своей дочери.Он решает построить пандус с трапециевидной поверхностью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:
| площадь = | × 9 = 173,376 кв. Футов |
Круг
Круг — это простая замкнутая форма, образованная множеством всех точек на плоскости, находящихся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки круга называется радиусом.Более подробную информацию о кругах можно найти на странице калькулятора круга, но для вычисления площади необходимо только знать радиус и понимать, что значения в круге связаны математической константой π . Уравнение для вычисления площади круга выглядит следующим образом:
площадь = πr 2
Фермер и его дочь — Круг Ли (ж)
Прошло еще шесть лет, и его дочь превратилась в сильного, красивого, влиятельного, уверенного в себе 15-летнего неблагодарного человека, сосредоточенного исключительно на поиске внешнего подтверждения со стороны знакомых и незнакомых людей в социальных сетях, при этом полностью игнорируя искреннюю поддержку со стороны ближайших родственников и друзей. .После спора с отцом по поводу чрезмерного использования социальных сетей, она решает использовать страх отца перед неизвестным и веру в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она ходит по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также на многие другие темы, которые игнорируйте все научные и логические объяснения.Убедившись, наконец, в сферической природе Земли, удалив все свои прошлые посты в социальных сетях, касающихся BoB, и расширив свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических кругов и хочет определить площадь, необходимую для создания кругов на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:
площадь = π × 15 2 = 706,858 кв. Футов
К несчастью для фермера, он не только напуган кругами на полях, которые появились в ту ночь, когда его дочь сказала ему, что она была на вечеринке со своими друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем своей дочери), но количество «исследователей круга» и «цереологов», появившихся на его ферме, чтобы изучить и впоследствии подтвердить подлинность кругов на полях как инопланетного сооружения, стоило ему значительного ущерба для его посевов .
Сектор
Сектор круга — это, по сути, часть круга, заключенного между двумя радиусами и дугой. Зная радиус и угол, площадь сектора можно вычислить, умножив площадь всего круга на отношение известного угла к 360 ° или 2π радианам, как показано в следующем уравнении:
| площадь = | × πr 2 | , если θ в градусах |
или
| площадь = | × πr 2 | , если θ в радианах |
Фермер и его дочь — разделение семьи
Фермер и его семья столкнулись с самой серьезной дилеммой на сегодняшний день.Прошел год, дочери фермера исполнилось 16 лет, и в рамках празднования ее дня рождения ее мать испекла ее любимый десерт — ежевичный пирог. К несчастью для дочери фермера, ежевичный пирог также является любимой едой их домашнего енота, Утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками виновника в виде крошек, ведущих к чрезмерно увлеченному еноту. Изначально пирог легко можно было разделить между тремя людьми и одним енотом, но теперь половину пирога приходится делить между тремя людьми, поскольку огорченный, но пресыщенный Утконос наблюдает издали.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом:
площадь = 60 ° / 360 ° × π × 16 2 = 134,041 дюйм 2
В результате невнимательности Утконоса каждый получает на треть меньше, и дочь задумчиво вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дэви Крокетта и его шляпы из енотовидной шкуры.
Эллипс
Эллипс — это обобщенная форма круга и кривая на плоскости, где сумма расстояний от любой точки кривой до каждой из двух ее фокальных точек постоянна, как показано на рисунке ниже, где P — любая точка эллипса, а F 1 и F 2 — это два фокусировки.
Когда F 1 = F 2 , полученный эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, который является частью калькулятора, является самым длинным радиусом эллипса, а малая полуось — самым коротким.Большая и малая оси относятся к диаметрам, а не радиусам эллипса. Уравнение для вычисления площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном месте для круга):
area = πab
, где a и b — мажор
и малые полуоси
Фермер и его дочь — падение с орбиты
Прошло два года с момента загадочного исчезновения домашнего питомца, Утконоса, и случайного выигрыша пушистого аксессуара дочери фермера в школьной лотерее, которая помогла заполнить пустоту потери их любимого питомца.Дочке фермера сейчас 18, и она готова сбежать из сельской Монтаны, чтобы жить в колледже, полной свободы и распутства, и, конечно же, немного поучиться на стороне. К несчастью для дочери фермера, она росла в среде, наполненной позитивным подкреплением и, следовательно, с менталитетом, что нужно «стрелять на луну, [поскольку] даже если вы промахнетесь, вы приземлитесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, что ей заблагорассудится! Таким образом, с ее неоптимальными оценками, отсутствием какой-либо внеклассной деятельности из-за ее бесчисленного множества различных интересов, отнимающих все ее свободное время, нулевого планирования и ее настойчивого стремления поступать только в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из ведущих университетов, в которые она подавала документы, что можно было бы разумно сравнить с ее метафорической посадкой в глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд.Наряду с ее легкими ее мечта стать астрофизиком была вкратце сорвана, по крайней мере, на время, и ей пришлось вычислить эллиптическую площадь, необходимую в ее комнате, чтобы построить модель почти эллиптической орбиты Земли вокруг Солнца размером с человека. чтобы она могла с тоской смотреть на солнце в центре своей комнаты и его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, с далеким вращением Земли, насмешливо представляющим расстояние между ее мечтами и твердой землей .
площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов
Параллелограмм
Параллелограмм — это простой четырехугольник, который имеет две пары параллельных сторон, причем противоположные стороны и углы четырехугольника имеют равные длины и углы. Прямоугольники, ромбы и квадраты — это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которые в дальнейшем можно преобразовать в прямоугольник, что делает уравнение для вычисления площади параллелограмма по существу таким же, как и для вычисления прямоугольника.Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Исходя из рисунка ниже, уравнение для вычисления площади параллелограмма выглядит следующим образом:
площадь = b × h
Фермер и его дочь — Алмаз в небе
Прошло еще два года в жизни фермера и его семьи, и, хотя его дочь была причиной сильного беспокойства, она наконец преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество. она должна оставаться на земле.В результате борьбы, которая последовала за ее добровольной изоляцией, в окружении воображаемых, осуждающих глаз, предполагающих ее неудачу со всех сторон, дочь фермера вышла из-под натиска земли, как алмаз, сияя ярко и твердо в своей решимости. Несмотря на все недостатки, она решает, что у нее нет другого выбора, кроме как продержаться через астероидное поле жизни в надежде, что финал сказки Диснея существует. Наконец-то, к счастью для дочери фермера и ее семьи, надежда действительно появилась, но не в виде Прекрасного Принца, а скорее как знак с предполагаемых небес.Несмотря на все ее метафорические размышления и невзгоды, связанные с космосом, почти становится правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельскохозяйственные угодья, что она интерпретирует как представление ее путешествия, становления и возможного возвращения домой. Дочь фермера приступает к измерению площади одного из ромбовидных лиц своего недавно найденного символа жизни:
площадь = 20 футов × 18 футов = 360 квадратных футов
К несчастью для дочери фермера, появление огромного алмаза привлекло внимание со всего мира, и после достаточного давления она уступает человеку внутри себя и продает алмаз, само изображение ее жизни и души, какому-либо человеку. богатый коллекционер, и продолжает жить остаток своей жизни в щедрых удовольствиях, отказываясь от своих убеждений и теряясь в черной дыре общества.

 м.
м.