Как найти периметр комнаты: Расчет периметра комнаты — онлайн калькулятор

21.09.2021 автор alexxlab

Содержание

Как посчитать периметр комнаты?

Во время ремонта может возникнуть ситуация, когда необходимо знать точный периметр комнаты, например при покупке плинтуса или при расчете количества обоев и напольного покрытия. Сделать это просто, если помещение имеет стандартную форму. Но что делать, если нам нужно произвести расчет для коридора, который имеет множество углов, или для спальни необычной формы? В этом процессе помогут некоторые хитрости, прибегнуть к которым можно при планировании ремонта.

Расчет для стандартных помещений: квадрат и прямоугольник

Чаще всего встречаются помещения, стены которых образуют прямоугольник или квадрат. В данном случае нам понадобятся:

рулетка;
линейка;
нитка;
бумага и карандаш.

Для начала вспомним, что такое периметр. Это геометрическая величина, являющаяся суммой длин всех сторон фигуры. Высчитать его еще проще, чем площадь пола.

Самый простой случай – это помещение, представляющее собой квадрат, то есть все его стороны равны.

Тогда измеряем одну сторону квадрата, приложив рулетку к стыку стены и пола.

Если у вас нет рулетки, используйте нитку, сделав отрезок, соответствующий расстоянию от угла до угла помещения, и измерьте его с помощью линейки.

Искомую величину можно посчитать, умножив результат измерения на 4. Так, для спальни, имеющей форму квадрата со стороной, равной 5 метрам, периметр будет равен:

5 х 4 = 20 (м)

Немного интереснее, когда комната является прямоугольником. Это означает, что длины противоположных стен равны между собой. В таком случае меряем расстояние от угла до угла двух смежных стен рулеткой, складываем полученные числа между собой и умножаем на 2. Для наглядности рассмотрим пример: дана гостиная прямоугольной формы, длина одной ее стены равна 5 метрам, другой – 5,5 м. Тогда периметр будет равен:

(5 + 5,5) х 2 = 21 (м)

Не забывайте, что даже при точном расчете количества стройматериалов их нужно покупать с небольшим запасом на случай порчи.

Нестандартные варианты: многоугольник и круг

Легко рассчитать периметр, когда противоположные стороны фигуры равны между собой. Усложним ситуацию: у имеющейся кухни больше четырех углов. В таком случае придется замерить каждый отрезок от одного угла до другого, после чего сложить все результаты измерений. Данный способ отличается от предыдущего тем, что для того чтобы рассчитать периметр, нужно больше исходных данных.

Возьмем кухню, имеющую форму шестиугольника с нишей. Тогда количество стен, которые нам придется измерить, сложив затем полученные значения, будет равно 8.

Усложним ситуацию еще больше: зал представляет собой окружность. Тут не поможет замер от угла до угла, так как их просто нет. Если существует уверенность, что это действительно круг, а не эллипс, то поможет знание геометрии. Периметр представляет собой длину окружности. А длина окружности, в свою очередь, является произведением диаметра окружности на число π.

Звучит страшно, но на самом деле все просто.

Находим центр комнаты и обозначаем его.
Закрепляем нитку у одной стены и проводим до противоположной через центр помещения.
Измеряем длину полученного отрезка. Это и есть диаметр окружности.

Теперь нужно считать. Берем полученный диаметр и умножаем на число π. Все знают, что данное число бесконечно большое. Но нам не нужна точность до сотых миллиметра, поэтому берем 3,14. Таким образом, периметр окружности является длиной отрезка от стены до стены через середину комнаты, умноженной на 3,14.

Значит, имея круглое помещение диаметром 5 метров, мы получим нужное нам значение следующим образом:

5 х 3,14 = 15,7 (м)

Полезные советы

Что делать, если совершенно не хочется считать или нет желания ползать по комнате, вымеряя рулеткой стены? Есть несколько полезных советов:

Возьмите у знакомого лазерную рулетку. С этим устройством можно будет провести все замеры самостоятельно, в отличие от рулетки, при использовании которой нужен товарищ, удерживающий ее конец. Кроме того, прибор выдаст более точный результат, так как лазерный луч не будет отклоняться. Это поможет точнее рассчитать периметр комнаты.
Используйте длинную нитку. Гораздо удобнее будет крепить части нитки к углам, не прерывая замер. Нитка должна разматываться до тех пор, пока не встретится собственным концом – началом замера. Её конечная длина – это и есть искомое значение. Такой способ поможет при наличии помещения, имеющего форму эллипса, так как по-другому рассчитать длину данной фигуры будет проблематично.

Таким образом, за небольшое время можно провести все необходимые замеры и получить готовый результат. Однако стоит помнить, что в результате нужно учитывать погрешность, чтобы не закупить стройматериала меньше, чем нужно. Например, если стена неровная, даже при точных расчетах в итоге потребуется больше плинтуса для сглаживания недочетов.

Как посчитать периметр комнаты 🚩 как самому рассчитать периметр комнаты 🚩 Квартира и дача 🚩 Другое

Вам понадобится

— рулетка;
— карандаш и бумага;
— нить.

Инструкция

Вспомните, что периметр – это не что иное как сумма длин всех сторон какой-то геометрической фигуры. И замечательно, когда та комната, в которой следует произвести расчеты , имеет стандартную форму, скажем квадрата или прямоугольника. В этом случае достаточно вспомнить школьную программу. К примеру, если комната квадратная, то для расчета ее периметра измерьте длину одной стороны и полученный результат умножьте на четыре. Итоговое число и будет периметром вашей комнаты.

Найдите длины двух прилегающих стен и сумму этих чисел умножьте на два, если комната прямоугольная. В результате получается периметр этого помещения.

Измерьте все прямолинейные отрезки и суммируйте полученные результаты, если комната имеет какую-то другую произвольную форму, что довольно часто сегодня встречается.

Порой бывает так, что комната имеет форму круга. Если вы точно уверены в том, что помещение круглое, то измерьте его диаметр, то есть расстояние от одной точки окружности до другой, пройдя через центр. А затем воспользуйтесь формулой, в которой периметр будет не что иное как диаметр окружности, умноженный на постоянную величину 3,14.

Все вышеописанные способы являются правильными. Но вот в чем проблема – не всегда помещения соответствуют всем техническим требованиям и стандартам, а именно бывает так, что длина одной стены отличается от длины противоположной стены. Для таких случаев в арсенале имеется совершенно простой и действенный способ расчета периметра комнаты.

Возьмите обычную нить как можно длиннее, и проложите ее по всей линии периметра. То место, где она сомкнется с началом отсчета, необходимо отметить. А затем измерьте полученную длину. Итог этого измерения и будет периметром вашей комнаты.

Как найти периметр прямоугольника — Лайфхакер

Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.

Зная все или две соседние стороны

Для полноты упомянем простейшие классические формулы.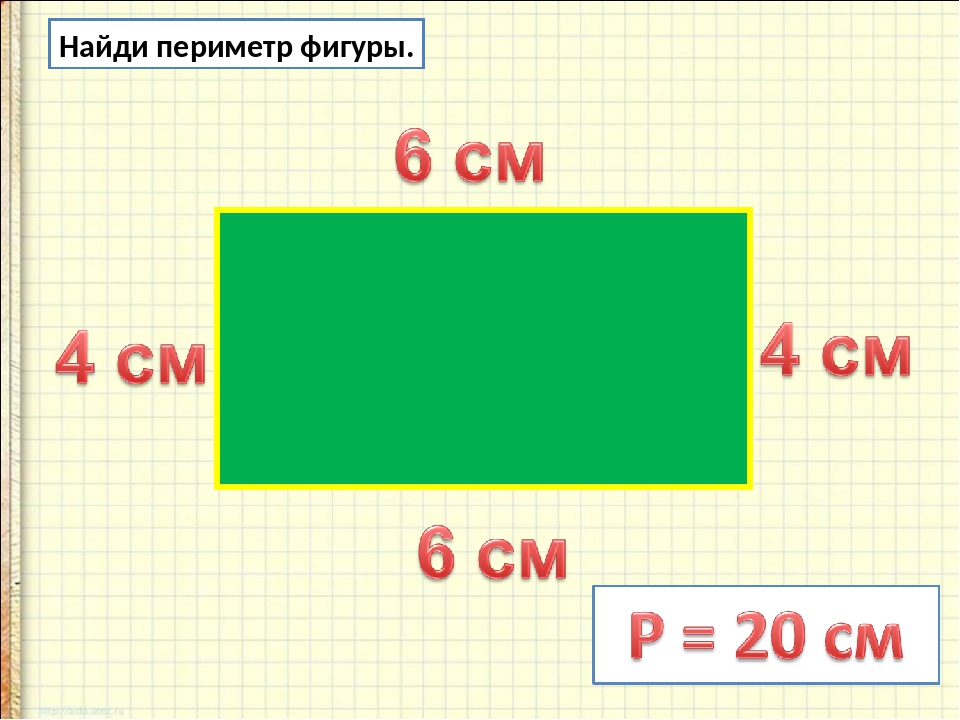

Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.

P — искомый периметр;
a, b, c, d — стороны прямоугольника.

Сейчас читают 🔥

Зная любую сторону и площадь

Поделите площадь на длину известной стороны.
Прибавьте результат к известной стороне.
Умножьте полученное число на два.

P — искомый периметр прямоугольника;
a — известная сторона;
S — площадь прямоугольника.

Зная любую сторону и диагональ

Посчитайте разность квадратов диагонали и стороны.
Найдите корень из результата.
Прибавьте полученное число к известной стороне.
Умножьте результат на два.

P — искомый периметр прямоугольника;
a — известная сторона;
d — диагональ прямоугольника.

Зная одну любую сторону и радиус описанной окружности

Умножьте квадрат радиуса на четыре.
Посчитайте разность полученного числа и квадрата известной стороны.
Найдите корень из результата.
Прибавьте полученное число к известной стороне.
Умножьте результат на два.

P — искомый периметр прямоугольника;
a — известная сторона;
R — радиус окружности, описанной вокруг прямоугольника.

Читайте также 📐✂️📌

Как найти периметр и площадь неполной фигуры. Что такое периметр

Любое важное начинание надо просчитывать заранее, ремонт не исключение. Поскольку затраты предстоят большие, надо их оптимизировать и уменьшить по максимуму, особенно, если хочется сделать что-то дорогостоящее, например натяжные потолки с несколькими уровнями. Если покупать материалы «на глазок», легко можно ошибиться – купить или слишком много или придется идти в магазин и докупать недостающие стройматериалы. Для того, чтобы не купить лишнего дорогого стройматериала и сэкономить семейный бюджет, надо знать, как рассчитать площадь помещения. Вот с этого то и начнем.

В каких случаях нужны расчеты?

Расчет квадратных метров обязателен, если в проекте установить подвесные потолки. Для наглядности посмотрим, что нужно для гипсокартонных конструкций. Площадь комнаты рассчитывается, чтобы закупить гипсокартон в нужном количестве, а периметр надо знать для покупки пристенного профиля для установки обрешетки. Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.

Для заказа натяжного потолка делать расчет квадратуры комнаты требуется, что запланировать будущие траты и проконтролировать фирму-установщика в правильности их расчетов. Фирма, изготавливающая натяжные потолки обычно указывает цену за квадратный метр и плюсует работу по установке. Зная площадь и стоимость квадрата, можно легко определить конечную цену.

Вычислить площадь требуется даже для банальной покраски пола или потолка, чтобы знать, сколько закупать краски. Важно купить нужное количество краски, иначе если не хватит, а краску в магазине колорировали, то можно не угадать с цветом. Примерный расход краски на метр квадратный поверхности указывается на банке.

Пример расчета потребности в краске:

Квадратура пола составляет 30 м2

расход краски согласно данным на упаковке – 0,20 кг/м2

30 х 0,2 = 6 кг

Полагается брать краску свыше расчетного количества на 10%.

Поэтому получаем 6 + 10% = 6,6 кг. Это подойдет ведро 7 кг или приближенная расфасовка в зависимости от вида краски.

Как посчитать площадь комнаты

Если вы владелец небольшой прямоугольной комнаты, то большого труда вычислить квадратуру комнаты это не составит. Достаточно вспомнить школьный курс геометрии. А что делать, если на месте потолка сложный многоугольник или имеются всевозможные ниши или выступы?

Прямоугольная комната

Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса. К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м. Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.

Комната сложной формы

Очень часто в домах старой постройки встречаются комнаты с нишами, выступами, встроенными кладовками. Нам предстоит решить задачку посложнее, но оказывается все просто. Потребуется лист в клетку или простой, на котором мы нарисуем эскиз комнаты с приблизительным сохранением пропорций. Далее измеряем метраж прямых стен и записываем на эскизе рядом с соответствующими линиями, обозначающими стены.

А вот теперь порисуем. Эскиз надо разбить на прямоугольники при помощи угольника и линейки, соблюдая прямые углы. Причем, одной из сторон прямоугольника должна быть измеренная полная стена. Теперь надо вычислить квадратные метры каждого из нарисованных прямоугольников и суммировать их. Периметр вычислить в любом случае проще – просто складываем длины всех стен и закоулочков.

Расчет площади многогранной комнаты

Что делать, если в комнате есть «срезанные» или не прямые углы? Нам предстоит задача в три действия, но сначала опять же замеряем все стены, не забывая про скосы, и рисуем эскиз. Вот, как этот к примеру.

Теперь начинается чистая геометрия. Первое действие – принимаем наш скос за гипотенузу прямоугольного треугольника, соединяем катеты. Остается применить формулу для вычисления прямоугольного треугольника, которая выглядит следующим образом: S = катет х катет /2. Катет у нас вычисляется так: известная длина стены равная 1,75 м (см. чертеж) минус противоположная стена 1,18 м. Получаем 0.57 м. Аналогично вычисляем другой катет, используя длины других противоположных стен.

Исходя из этого найдем площадь треугольника 0,57 х 0,57 / 2 = 0.57 м2

Второе действие – разделение комнаты на два прямоугольника без учета уже посчитанного треугольника. См. рисунок.

В заключение

Не стоит скрупулезно обмерять и высчитывать все значения. В любом случае будет погрешность около 5%, но сколь либо серьезно это значение не влияет на расчеты. Можно не брать во внимание небольшие скругления углов. Если надо рассчитать площадь стен для закупки отделочных материалов, то действуем по первому примеру с правильным прямоугольником, вычитая площадь окон и дверей. В наших домах стандартная высота потолков может разниться в каждом из углов, поэтому берем большее значение с учетом обрезки. Пусть лучше будет небольшой запас, чем потом думать, как выйти из ситуации. Удачи вам в ремонте!

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой

P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Площадь и периметр – две численные характеристики, часто используемые в геометрии. Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).

Определение

Площадь – величина, характеризующая размер поверхности, которую занимает геометрическая фигура.

Периметр – размер границ (контура) геометрической фигуры.

Понятия применимы для каждой геометрической фигуры и выражаются в различных единицах. Расчет периметра и площади определяется единицами измерения параметров, используемых для их вычисления: длин сторон, диаметра, высоты. В геометрии указанные параметры чаще всего измеряются в мм, см, м.

Сравнение

Периметр обозначается заглавной буквой P , используется при измерении многоугольников и определяется как сумма длин его сторон. Площадь обозначается буквой S и может быть использована как численная характеристика поверхности, имеющей различный контур, в том числе искривленный. Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.

Простейший случай – квадрат. Длины его сторон равны, поэтому для вычисления периметра достаточно умножить одну сторону на 4. Формула выглядит так:

Р = a + a + a + a = a х 4, где а – сторона квадрата.

Для вычисления площади квадрата используется другая формула:

S = a х a = a 2 .

Выводы сайт

В случае с периметром речь идет о размерах контура, в случае площади – о размерах поверхности.
Единица измерения S определяется как квадрат единицы измерения характеристик поверхности, для периметра она равна единице измерения сторон многоугольника.
Периметр характеризует размеры многоугольника, площадь – более широкое понятие, применимое для поверхностей с различным контуром.
Формулы для определения площадей сильно различаются, а для определения периметра достаточно просто сложить стороны многоугольника.

Подписаться на сайт

Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P . Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Ответ: 40 см

P = 10+10+10+10

P =40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S= 100 см 2

Ответ: 10 0 см 2

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P = (6+2) * 2

P = 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S = 5*2

S =10см 2

Ответ: 10 см 2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L = 2*3,14*3

L =6 π

L=6*3.14

L = 18.84 см

P к = 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.

На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.

Рассмотрим следующую геометрическую фигуру (рис. 1):

Рис. 1. Прямоугольник

Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.

Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.

Рассмотрим следующую задачу:

Задача 1 (рис. 2)

Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?

Рис. 2. Иллюстрация к задаче 1

Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.

Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.

Ответ: 30 метров.

Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).

Периметр любой фигуры измеряется в линейных единицах.

На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.

Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.

Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).

Список литературы

Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.

Festival.1september.ru ().
Nsportal.ru ().
Math-prosto.ru ().

Домашнее задание

Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
Найти периметр прямоугольника, если его полупериметр — 21 дм.

Урок 49. периметр прямоугольника — Математика — 2 класс

Математика, 2 класс. Урок № 49

Периметр прямоугольника

Перечень вопросов, рассматриваемых в теме:

Изучение правила вычисления периметра прямоугольника.

Глоссарий по теме:

Прямоугольник – четырёхугольник, у которого все углы прямые.

Периметр – сумма длины всех сторон плоской фигуры.

Основная и дополнительная литература по теме урока:

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –

8-е изд. – М.: Просвещение, 2017. – с.16.

2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова –

7-е изд., дораб. – М.: Просвещение, 2016. – с.22.

Открытые электронные ресурсы по теме урока:

Интересные факты о математике. Познай мир. URL:

https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/ (дата обращения: 18.08.2018)

Теоретический материал для самостоятельного изучения

Прямоугольные предметы окружают нас повсюду.

Рамки, телефоны, тетради и многое другое.

Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны.

Рассмотрим следующую задачу: «Вокруг дачного участка необходимо поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится?»

Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.

длина

ширина

длина

У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров.

Составим выражение для подсчета длины забора. Это первый способ вычислений: 5 + 10 + 5 + 10

Воспользуемся переместительным законом сложения:

5 + 10 + 5 + 10 = 5 + 5 + 10 + 10

В данном выражении есть суммы одинаковых слагаемых

5 + 5 и 10 + 10

В этой записи рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно заменить умножением. Это второй способ вычислений:

5 + 5 + 10 + 10 = 5 · 2 + 10 · 2

Теперь воспользуемся распределительным законом умножения относительно сложения. Это третий способ вычислений: 5 · 2 + 10 · 2 = (5 + 10) · 2

Этот способ можно назвать рациональным, то есть, наиболее удобным и коротким, потому что в нём меньше действий, чем в предыдущих способах.

Найдём значение выражения (5 + 10) · 2

Сначала выполняем действие в скобках: 5 + 10 = 15

А затем повторяем число 15 два раза: 15 · 2 = 30.

Ответ: 30 метров забор вокруг участка.

Забор вокруг участка — это периметр этого участка. Периметр прямоугольника – сумма длин всех его сторон.

Делаем вывод: периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.

Тренировочные задания.

1. Решите задачу: Длина листа картона 4 см. Ширина 3 см. Вычислите периметр данного листа. Запишите решение тремя способами.

Правильный ответ:

1 способ. 4+3+4+3=14 (см)

2 способ. 4 · 2+ 3·2=14 (см)

3 способ. (4+3) ·2=14 (см)

Ответ: 14 сантиметров периметр листа картона.

2. Выберите верное решение:

Длина прямоугольника 5 см, ширина 3 см. Чему равен периметр прямоугольника?

А) 8 см Б) 13 см В) 16 см

Правильный ответ В) 16 см

Как измерить периметр фигуры. Периметр квадрата и прямоугольника. Способы определения и примеры решения. Подготовка к изучению нового материала

Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:

Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.

Периметр – это общая длина всех сторон фигуры.

Вычисление периметра прямоугольника — довольно простая задача.

Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.

Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.

P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.

Так же периметр прямоугольника можно найти при помощи суммы всех сторон.

P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.

Периметр квадрата — это длина стороны квадрата, умноженная на 4.

P = a 4, где a — длина стороны квадрата.

Дополнение: Нахождение найти площади и периметра прямоугольников

В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.

Основные понятия

Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:

Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
Квадрат. Является четырехугольником, все стороны которого равны.

При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.

Вычисление периметра

Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.

Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».

Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.

Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).

Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».

Ответ: P=5+4+3=12 (см).

Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».

Ответ: P=7+9+7+9=32 (см).

Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».

В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.

Ответ: 50 (м).

Вычисление площади

Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.

Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².

Области применения единиц измерения могут быть такими:

В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
В дм² можно измерить географическую карту, оконное стекло, картину.
Для измерения пола, квартиры, земельного участка используют м².

Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.

Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.

Способы сравнения площадей:

На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².

Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».

Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.

Ответ: 30 (м).

Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».

Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).

Ответ: 18 (м²).

Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Что такое прямоугольник и квадрат

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

Что такое площадь прямоугольника?

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

Периметр — это сумма длин всех сторон многоугольника.

Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

Прямоугольник – это четырехугольник.
Все параллельные стороны равны
Все углы = 90º.
Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

1 способ. Складываем все стороны. P = a + а + b + b
2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

: a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Не многие формулы из курса школьной математики мы применяем в повседневной жизни. Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.

Что такое периметр?

Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.

Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.

Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.

Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.

Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.

Прикладное значение периметра

Вычисление периметра в повседневной жизни применяется во многих сферах, но чаще всего при выполнении строительных, геодезических, топографических, архитектурных, планировочных работах. Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.

Например, при выполнении геодезических и топографических работ очень часто возникает необходимость посчитать периметр границ определенного участка. Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.

Необходимость вычисления периметра участка очень часто обусловлена тем, что необходимо знать, какое количество материала потребуется для установки ограждений. Даже простой приусадебный участок нуждается в измерении периметра для того, чтобы грамотно обнести его забором.

Измерительные приборы на местности

Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант — это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.

Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.

Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.

Как рассчитать периметр комнаты — Наука

Наука 2021

Содержание:

Если вас когда-либо отправили в свою комнату для наказания, вы, возможно, обошли его периметр от скуки. Периметр объекта — это измерение границ его площади. Подобно определению площади комнаты, определение ее периметра требует от вас измерения длины стен; но в отличие от области, периметр касается только границ пространства.

Умножьте длину одной стены на 4, чтобы вычислить периметр квадратной комнаты, так как все четыре стороны квадрата имеют одинаковую длину по определению. Думайте о полу как о квадрате. Например, предположим, что длина одной стены составляет 20 футов. 20, умноженное на 4, дает периметр 80 футов.

Удвойте измерения ширины и длины и сложите их вместе, чтобы вычислить периметр прямоугольной комнаты. Например, предположим, что длина комнаты составляет 18 футов, а ширина — 14 футов. Удвоение 18 приводит к 36, а удвоение 14 — к 28. Сложение 36 и 28 вместе составляет 64 фута.

Суммируйте длины трех стен вместе, чтобы вычислить периметр треугольной комнаты. Например, длина стен составляет 15 футов, 20 футов и 20 футов. Сложение этих длин вместе дает периметр 55 футов.

Умножьте диаметр круглой комнаты на пи, чтобы вычислить ее периметр. Диаметр круга — это расстояние от одной стороны до другой, проходящее через центр. Pi, или π, является неповторяющейся математической константой в виде десятичной дроби, которая начинается с 3.14159. Например, предположим, что диаметр комнаты составляет 20 футов. Умножение 20 на π дает округленный периметр 62.832.

Суммируйте длины всех стен, чтобы вычислить периметр любой комнаты. Например, предположим, что в комнате есть две изогнутые стены размером 18 и 20 футов и три прямые стены размером 18, 24 и 15 футов. Добавление этих чисел приводит к периметру 95 футов.

периметр комнаты 40 футов. длина комнаты в полтора раза больше ее ширины. найти размеры комнаты.

Мария Л.
задано • 19.09.17
Я знаю, что периметр 40 футов.
Кэрол Х. ответил • 19.09.17
Опытный преподаватель математики со степенью магистра математики
Пусть w = ширина
Пусть 3/2 w = длина
P = 2l + 2w
40 = 2 (3/2 Вт) + 2 Вт
40 = 3 Вт + 2 Вт
40 = 5 Вт
8 футов = ширина
длина = (3/2) ширина = (3/2) (8)
длина = 12 футов
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈〉 ◊
Как найти периметр прямоугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти периметр из области — Видео и стенограмма урока
Периметр квадрата
Давайте начнем с квадрата и изучим этот пример задачи.Найдите периметр квадрата площадью 64 квадратных метра.
Шаг 1
Запомните формулы для площади и периметра квадрата. Площадь квадрата равна a = s 2, или сторона, умноженная на сторону, а периметр равен p = 4 s , или в 4 раза s .
Шаг 2
Найдите длину одной стороны, подставив значение площади в формулу и решив для s. В данном случае 64 = с 2, поэтому с = 8.
Шаг 3
Подставьте значение s (длина стороны) в формулу периметра и решите.
p = 4 x 8, поэтому p = 32
Периметр круга
Затем давайте рассмотрим пример задачи, чтобы найти периметр круга по его площади. Найдите периметр круга площадью 9 пикселей.
Шаг 1
Запомните формулы для площади и периметра круга. Площадь круга составляет a = pi * радиус 2, а периметр круга, более известный как окружность , составляет p = 2pi * radius.
Шаг 2
Найдите длину радиуса, подставив площадь и решив формулу
9pi = pi * r 2
Разделите на пи, чтобы получить: 9 = r 2
r = 3
Шаг 3
Подставьте значение r в формулу периметра
p = 2 * pi * 3
p = 6pi
Периметр прямоугольника
Невозможно определить периметр прямоугольника, учитывая только площадь.Площадь прямоугольника зависит от двух неизвестных, длины и ширины, поэтому вам необходимо указать хотя бы одну сторону прямоугольника вместе с площадью, чтобы определить другую сторону и, таким образом, периметр.
Рассмотрим пример задачи. Найдите периметр прямоугольника длиной 4 и площадью 36м2.
Шаг 1
Запомните формулу для периметра и площади прямоугольника. Площадь прямоугольника составляет a = длина * ширина, а периметр равен p = (2 * длина) + (2 * ширина)
Шаг 2
Подставьте известные значения в формулу площади
36 = 4 * w
36/4 = w
w = 9
Шаг 3
Подставьте значения длины и ширины в формулу периметра.
p = 2 * 4 + 2 * 9
p = 8 + 18 = 26
Форматирование ответов
Ответы для каждого из этих вычислений будут в стандартных единицах , а не в квадрате. Вы должны использовать то же измерение, что и в исходной задаче, чтобы отформатировать свой ответ.
В примере задачи нахождения периметра квадрата площадь была указана в квадратных метрах, поэтому периметр должен быть указан в метрах. Таким образом, ответ — 32м.Если исходная задача не дает результатов, в ответе не следует использовать никакие измерения.
Как и в случае с квадратом, ответ для периметра круга должен быть дан в стандартных единицах исходной меры, если не была указана никакая мера. В этом примере измерения не проводились, поэтому ответ — 6 * пи. Обычно используется значение числа Пи 3,14159, поэтому также можно вычислить 6 * 3,14159, чтобы получить 18,84954 в качестве ответа на периметр этого круга.
Как и в других примерах, с прямоугольником, если площадь дана в квадратах, периметр должен быть в стандартных единицах.Здесь правильно отформатированный ответ — 26м.
Советы для всех правильных форм
Помните, что правильных форм — это формы с равными сторонами. Чтобы найти периметр правильной формы из области этой формы, вам необходимо знать формулы для площади и периметра формы.
Шаг 1 — подставить площадь в формулу площади и найти длину одной стороны. Поскольку это правильная форма, вы знаете, что все стороны равны.
Шаг 2 — подставить значение стороны в формулу периметра и решить.
Шаг 3 просто обеспечивает правильное форматирование ответа. Периметр всегда указывается в стандартных единицах.
Результаты обучения
После завершения этого урока учащиеся должны уметь:
Вычислять периметр квадрата, круга и прямоугольника с использованием площади
Вспомните, как форматировать вычисления периметра
Как измерить периметр ковра | Home Guides
Измерение ковра — это немного сложнее, чем вы думаете, но это не так уж сложно.Если только комната не очень маленькая, это больше, чем просто обмерить комнату и купить рулон ковра. Большинство комнат не имеют идеальных пропорций, и большая часть ковров изготавливается стандартной ширины. Чтобы получить нужное количество ковра, вам необходимо знать площадь в квадратных футах, квадратные метры и иметь достаточно точную схему комнаты. Самостоятельное измерение может помочь вам оценить стоимость, но ваш установщик может захотеть измерить еще раз, прежде чем вы купите ковер.
Измерьте расстояние вдоль одной стены от угла до угла.Если комната имеет необычные углы и не является достаточно близким квадратом или прямоугольником, измерьте самую длинную стену в комнате.
Измерьте вдоль любой стены, перпендикулярной первой стене, которую вы измерили. Если одна из перпендикулярных стен короче другой, измерьте длину более длинной стены.
Умножьте размер от первой стены на размер от второй стены, чтобы определить приблизительную площадь комнаты в квадратных футах. Если одна стена имеет длину 15 футов, а перпендикулярная стена — 10 футов, размер комнаты составляет приблизительно 150 квадратных футов.
Разделите квадратный метр комнаты на девять, чтобы определить квадратный метр. Ковровые покрытия обычно продаются квадратными ярдами, а не квадратными футами. Площадь комнаты 150 квадратных футов составляет 16,67 квадратных ярда.
Определите приблизительное количество необходимого ковра, нарисовав диаграмму на миллиметровой бумаге. Присвойте одному квадрату на миллиметровой бумаге числовое значение в футах или ярдах. При рисовании на миллиметровой бумаге ноги обычно более точны, чем ярды. Нарисуйте контур комнаты на миллиметровой бумаге, используя квадраты в качестве ориентира для каждой стены.Например, если одна стена имеет длину 15 футов, нарисуйте линию для одной стены на бумаге длиной в 15 квадратов и повторите для каждой стены, пока не создадите контур или периметр комнаты на бумаге.
Укажите размеры в квадратных футах и квадратных ярдах вместе со схемой помещения в качестве ориентира для продавца при покупке ковров. Продавец ковров будет использовать ваши расчеты, чтобы определить, сколько коврового покрытия необходимо для покрытия пола.
Ресурсы
Советы
Хотя примерная комната примерно 16.67 квадратных ярдов, 16.67 квадратных ярдов ковра могут не покрыть пол должным образом. Большинство ковров изготавливаются шириной 12 футов, а некоторые — шириной 15 футов. В комнате, которая шире и длиннее 12 футов, для большинства ковровых покрытий требуется шов, чтобы соединить две секции вместе, что означает покупку дополнительных ярдов коврового покрытия.
Высокая оценка при измерении и покупке ковра.
Окончательные расчеты продавца обычно включают покупку ковра на 10–20 процентов больше, чем вы думаете, что вам нужно.Разумно покупать больше, чем вам нужно, так как установщики ковров могут столкнуться с ситуацией, которую вы не учли.
Предупреждения
Не рекомендуется покупать ковровое покрытие, точно подходящее к комнате. Розничные продавцы обычно не могут забрать ковер, если он неправильно обрезан, исходя из ваших расчетов, а покупка пары дополнительных квадратных метров, чтобы компенсировать дефицит, может привести к образованию шва в странном месте.
Писатель Биография
Кэрол Олдройд, писатель из Восточного Теннесси, является автором множества статей по домашнему благоустройству, кадрам, кадрам и юриспруденции своими руками.Помимо получения степени в области параюридических исследований, она имеет более чем 10-летний опыт ремонта новых домов и восстановления исторической собственности.
Периметр и площадь | Математика для гуманитарных наук
Периметр
Периметр — это одномерное измерение, которое проводится вокруг внешней части замкнутой геометрической формы. Давайте начнем обсуждение концепции периметра с примера.
Управляемый пример
Рисунок 1.
Рисунок 2.
У Джозефа нет машины, поэтому он должен ездить на автобусе или идти пешком. По понедельникам он должен ехать в школу, на работу и снова домой. Его маршрут изображен на рисунке 1.
Очевидный вопрос, который следует задать в этой ситуации: «сколько миль проезжает Джозеф по понедельникам»? Для вычисления мы каждое расстояние: 3 + 6 + 6 = 15.
Джозеф проезжает 15 миль по понедельникам.
Другой способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и помеченную расстоянием от одного места до другого.
Обратите внимание, что маршрут Джозефа представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. Рисунок 2). Что мы можем спросить об этой форме: «каков периметр треугольника»?
Периметр означает «расстояние вокруг замкнутой фигуры или фигуры», и для вычисления мы складываем каждую длину: 3 + 6 + 6 = 15
Наш вывод тот же, что и выше: Джозеф проезжает 15 миль по понедельникам.
Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили конкретную геометрическую концепцию ( периметр ) к компьютеру, как далеко проехал Джозеф.
Записки по периметру
Периметр — это одномерное измерение, которое представляет собой расстояние вокруг замкнутой геометрической фигуры или фигуры (без промежутков).
Чтобы найти периметр, сложите длины каждой стороны фигуры.
Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. Д.).
Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рисунке 3 показана разница между закрытой фигурой и открытой фигурой.
Рисунок 3.
Пример 1
Найдите периметр для каждой из фигур ниже.
Сложите длины каждой стороны.
Иногда приходится делать предположения, если длина не указана.
Решения
12 шт.
40 футов
Пример 2
Как найти периметр этой более сложной формы?
Решение
Просто продолжайте добавлять длины сторон.6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 шт.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждый периметр в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали, приведенным ниже формулам.
Форма Периметр
Треугольник со сторонами, a , b , c : [латекс] P = a + b + c \\ [/ латекс]
Квадрат с длиной стороны a : [латекс] P = a + a + a + a \\ [/ latex]
[латекс] P = 4a \\ [/ latex]
Прямоугольник со сторонами a , b : [латекс] P = a + b + a + b \\ [/ латекс]
[латекс] P = a + a + b + b \\ [/ латекс]
[латекс] P = 2a + 2b \\ [ / латекс]
Окружность
Как вы понимаете, мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название, называемое окружностью .Чтобы найти длину окружности, воспользуемся этой формулой: C = 2πr
Рисунок 4.
В этой формуле π произносится как «пи» и определяется как длина окружности, деленная на ее диаметр: [latex] \ displaystyle \ pi = \ frac {C} {d} \\ [/ latex]. Обычно мы заменяем π приближением 3.14. Буква r представляет радиус круга.
Давайте посмотрим, откуда взялась формула для определения окружности. На рисунке 4 показан общий круг с радиусом r.
Примечания о
C = 2π r
Помните, что в формуле при вычислении длины окружности C = 2π r , мы умножаем , обычно , заменяя 3,14 вместо π:
C = 2 × 3,14 × r
Часто использование () помогает облегчить просмотр различных частей формулы:
С = (2) × (3,14) × ( r )
Происхождение
C = 2π r
Как упоминалось ранее, специальное число π определяется как отношение длины окружности к ее диаметру.Мы можем записать это в форме уравнения как: [latex] \ displaystyle \ frac {C} {d} = \ pi \\ [/ latex]
Из нашей предыдущей работы мы знаем, что для определения неизвестного, C , мы можем переместить d на другую сторону уравнения, написав C = π d. Диаметр полностью пересекает середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить C с точки зрения радиуса как C = π (2 r ). После небольшого изменения порядка, в котором написаны наши детали, мы можем сказать, что C = 2π r.
Давайте воспользуемся формулой, чтобы найти длину окружности нескольких окружностей.
Пример 3
Найдите длину окружности каждого из следующих кругов. Оставляйте свои ответы сначала в точном виде, а затем в округленном (до сотых разрядов). (Обратите внимание, что когда указан радиус, его значение центрируется над сегментом радиуса. Когда указан диаметр, его значение центрируется над сегментом диаметра.)
Решения
Точное значение 8π дюймов; округлено от точного ответа 25.13 дюймов; округлено с использованием 3,14 для π 25,12 из
Точное 12,44π м; округлено от точного ответа 39,08 м; округлено с использованием 3,14 для π 39,06 м
Точная форма и закругленная форма
π — число в точной форме. Он не округлый.
3,14 — это приближение округленной формы для π
Почему важно, какую форму мы используем? Это важно, потому что при округлении мы вносим ошибку в окончательный результат. Для этого класса такая ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, такой уровень точности имеет большое значение.Давайте посмотрим на примере разницы в формах.
Пример 4
Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную, так и округленную форму:
Точное решение
[латекс] C = 2 \ pi {r} = 2 \ pi (1079) = 2158 \ pi \\ [/ latex]
Чтобы округлить от до точного решения, используйте кнопку π на калькуляторе, чтобы получить
[латекс] 2158 \ pi \ приблизительно 6779,56 \ [/ латекс]
Округленное решение
[латекс] C = 2 \ pi {r} = 2 (3.14) (1079) \ приблизительно 6776,12 \ [/ латекс]
Обратите внимание, что наши окончательные результаты отличаются. Эта разница — ошибка, созданная при использовании 3,14 в качестве начального приближения для π. Выполняя домашнее задание и тесты, внимательно читайте инструкции по каждой задаче, чтобы понять, какую форму использовать.
Пример 5
Найдите длину окружности или периметра для каждой описанной ниже ситуации. Включите рисунок формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры рисовать.Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате. Округлите до десятых, если не указано иное.
Найдите периметр квадрата со стороной 2,17 фута.
Найдите периметр прямоугольника со сторонами длиной 4,2 и 3,8.
Найдите периметр треугольника со сторонами длиной 2, 5, 7.
Найдите длину окружности радиуса 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Представьте округлую форму с точностью до десятых.
Найдите длину окружности диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
8,68 футов
16
14
Точное 12π дюйма, округленное 37,7 дюйма
Точное 14,8π дюйма, Округленное 46,5 дюйма
Пример 6
Определение расстояния вокруг нестандартных форм
Основные формулы для периметра прямых фигур и окружности круга помогут нам найти расстояние вокруг более сложных фигур.Найдите расстояние вокруг следующей формы. Округлите окончательный ответ до десятых и используйте 3,14 вместо π.
Решение
34,7 дюйма
Пример 7
Аппликации периметра и окружности
Наши знания основных геометрических фигур могут быть применены для решения «реальных» задач.
Уолли хочет добавить забор позади своего дома, чтобы дети могли безопасно играть (см. Диаграмму ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерения перед тем, как пойти в магазин.Если он помнит, что длина задней стены его дома составляет 15 ярдов, есть ли у него достаточно информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов ему следует купить?
Решение
81 фут
Площадь
Давайте еще раз посмотрим на задний двор Уолли из примера 7, чтобы представить следующую концепцию: площадь.
Управляемый пример
Уолли успешно огородил свой двор, но теперь хочет добавить немного озеленения и создать лужайку, как показано ниже.
Он направляется в местный магазин по продаже газонов и обнаруживает, что для того, чтобы определить, сколько дерна ему нужно, он должен вычислить квадратные метры площади, на которой он хочет добавить траву. По пути домой он понимает, что если разделит травянистую территорию на участки размером 1 фут на 1 фут, а затем пересчитает их, он сможет определить площадь в квадратных футах. Вот информация, которую Уолли собрал, когда вернулся домой.
Уолли правильно определил, что площадь прямоугольного травянистого участка составляет 30 квадратных футов.
Заметки о зоне
Площадь — это двумерное измерение, которое представляет собой объем пространства внутри двухмерной фигуры.
Чтобы найти площадь, посчитайте количество единичных квадратов внутри фигуры.
Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут двухмерными (например, квадратные футы, квадратные ярды, квадратные мили и т. Д.).
Пример 8
Найдите область для каждой из фигур ниже.
Не забудьте посчитать единичные квадраты внутри фигуры.
Есть ли здесь шаблон, который облегчил бы нашу работу?
Пример 9
Как найти область для более сложных фигур? Разбейте области на формы, которые мы узнаем, и сложите значения областей вместе.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждую область в виде более явной формулы.2 \ [/ латекс] Прямоугольник со сторонами a , b
[латекс] A = a \ cdot {b} \\ [/ latex]
(Вы также увидите это как [latex] A = \ text {length} \ cdot \ text {width} \\ [/ latex])
Формулы площади для фигур ниже сложнее получить, поэтому формулы перечислены для вас в таблице.
Форма Форма
Треугольник высотой h и основанием b
[латекс] \ displaystyle {A} = \ frac {1} {2} bh = \ frac {bh} {2} \\ [/ latex]
Читается как «половина основания, умноженная на высоту»
Обратите внимание, что h — это расстояние по прямой от вершины треугольника до другой стороны.2 \ [/ латекс]
Читается как «пи, умноженный на радиус в квадрате»
Если ваш треугольник такой, как показано на рисунке слева, то высота нарисована и измерена за пределами треугольника.
Формула площади такая же.
Пример 10
Найдите область для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Используйте 3,14 для π и округлите ответы до десятых, если необходимо.
Найдите площадь прямоугольника, длина которого составляет 12,9 метра, а высота составляет одну треть этой величины.
Найдите площадь треугольника с основанием [latex] \ displaystyle {24} \ frac {1} {2} \\ [/ latex] дюймов и высотой 7 дюймов.
Найдите площадь круга с радиусом [latex] \ displaystyle {2} \ frac {1} {3} \\ [/ latex] дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
55,5 м ² или 55,5 кв.м (округлено)
85,8 дюйма ² или 85,8 квадратных дюйма (округлено)
Точное 49/9 π дюйма ², Округленное 17,1 дюйма ²
Пример 11
Найдите область в каждой описанной ситуации. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Округляйте ответы до десятых, если не указано иное.
Найдите площадь квадрата со стороной 4,2 фута.
Найдите площадь прямоугольника со сторонами длиной 4,2 и 3,8.
Найдите площадь треугольника высотой 7 дюймов и основанием 12 дюймов.
Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
17.64 фута ² или 17,64 квадратных футов
16,0
42 дюйма ² или 42 квадратных дюйма
Точное 36π на ² или 36π квадратных дюймов, округленное с использованием 3,14 для π 113,0 дюймов ² или 113,0 квадратных дюймов
Пример 12
Нахождение области нестандартных форм
Основные формулы площади помогут нам найти площадь более сложных фигур. Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь данной формы.Вычислить, используя 3,14 для π и округлить до ближайшей десятой.
Решение
Округлено с использованием 3,14 для π 25,9 дюйма ²
Пример 13
Применение площади и периметра
Мы можем объединить наши знания о площади / периметре для решения таких проблем, как эта.
Уолли все еще ремонтирует свой дом, и ему нужно завершить проект полов. Он хочет купить достаточно бамбукового пола, чтобы покрыть пространство в комнатах A, C и коридоре B, а также достаточно бамбуковой кромки для плинтусов во всех помещениях.Сколько квадратных футов пола и сколько футов плинтусов ему следует купить?
Решение
256 футов ² настил, 108 футов окантовка
Периметр неправильных форм — математика с мамой
Чтобы найти периметр неправильной формы, вы просто складываете длины внешних сторон формы.
В этом уроке мы рассмотрим несколько примеров неправильных форм и научимся рассчитывать их периметры.
Правильная форма — это форма, у которой все стороны имеют одинаковую длину.Все его углы также будут одинакового размера.
Неправильная форма — это просто любая форма, у которой не все сторон и углов одинаковы. Неправильная форма — это любая форма, которая не является правильной.
Мы называем неправильные формы в зависимости от того, сколько у них сторон. Поскольку количество углов у фигуры такое же, как и количество ее сторон, мы также можем назвать фигуру по количеству углов.
Ниже приведены несколько распространенных примеров неправильных форм, упорядоченных в виде списка, с указанием их свойств.
При обучении неправильным формам важно помнить о распространенной ошибке. Иногда люди думают, что для того, чтобы форма была неправильной, все ее стороны должны отличаться друг от друга. Однако форма является неправильной, если у нее есть хотя бы одна сторона, длина которой отличается от длины любой из других сторон.
Например, у треугольника могут быть две одинаковые стороны, но только одна сторона, которая отличается от двух других сторон, и это неправильная форма.
Ниже приведены несколько примеров неправильных форм.
Периметр формы — это общее расстояние вокруг ее внешних краев .
Чтобы рассчитать периметр формы , мы складываем длины каждой стороны .
Вот пример определения периметра неправильного треугольника:
Чтобы найти периметр этого неправильного треугольника, мы складываем длины трех сторон.
Совет по обучению периметру неправильных форм — зачеркнуть каждую сторону длины по мере того, как вы ее добавили.
Распространенная ошибка детей при вычислении периметра состоит в том, что они полностью пропускают сторону или считают сторону более одного раза.
Я рекомендую, чтобы во избежание этой ошибки вы могли научить ребенка выбирать угол для начала. Перемещайте внешнюю часть фигуры и зачеркивайте боковые стороны по мере добавления, если они достаточно просты для вашего ребенка. Вы можете рисовать вокруг исходной формы по ходу движения или выделять каждую сторону, пока не вернетесь к тому месту, где вы начали.
Однако для некоторых вопросов с большими числами это может привести к расчетам, которые не всегда проще всего выполнить в первую очередь.Вместо этого вы можете искать стороны, которые в сумме дают более простые числа, например, используя числовые связи, а затем просто перечеркивать эти стороны по мере их добавления.
В этом примере у нас есть только три стороны, поэтому мы будем просто скрещивать стороны при их добавлении.
8 + 10 = 18
18 + 5 = 23
Периметр этого треугольника равен 23 мм .
Помните, что периметр — это мера общей внешней длины фигуры, и ответ, который мы получаем, — это измерение длины.
Поэтому нашими единицами измерения будут единицы длины. Поскольку в нашем примере мы измерили каждую сторону в миллиметрах (мм), мы также добавили общую длину в миллиметрах.
Мы пишем «мм» после 23, чтобы показать, что у нас 23 миллиметра. «Мм» — это краткое обозначение миллиметров.
Точно так же, как мы ставим пробел между 23 и миллиметрами, мы ставим пробел между 23 и мм. Мы не будем писать «23 миллиметра», мы будем писать «23 миллиметра», и точно так же мы пишем «23 мм», а не «23 мм».Это правило оставлять пробел применяется ко всем единицам измерения.
Вот еще один пример определения периметра неправильного пятиугольника:
Как мы уже говорили ранее, эта форма будет неправильной, потому что не все ее стороны одинаковы.
Несмотря на то, что у него есть две стороны, равные 13 метрам, у него есть еще три стороны, которые все отличаются от этого. Это не регулярно, это нерегулярно.
Чтобы найти периметр этого пятиугольника, мы складываем длины каждой стороны вместе.
Чтобы убедиться, что мы не добавляем сторону более одного раза , мы вычеркнем стороны при их добавлении.
Мы также позаботимся о том, чтобы записывать наши расчеты, чтобы не ошибиться.
Длины сторон указаны в метрах. Вместо того, чтобы писать слово «метры» рядом с каждым числом, быстрее и проще писать «м». «М» — это сокращение от «метры», и мы пишем свое число, затем пробел и затем «м».
Мы можем начать с двух самых больших сторон, так как их будет не очень приятно добавлять позже к и без того большому количеству.
Две самые большие стороны имеют длину 13 метров, и, поскольку у нас их две, это означает, что мы можем удвоить 13, чтобы получить наш ответ.
Как правило, удвоение является более простой стратегией, чем сложение, и это еще один совет, на который следует обратить внимание при приближении к расчетам периметра. Мы можем найти любые одинаковые стороны и умножить длину на то, сколько сторон имеют эту длину.
13 + 13 = 26 (или 13 x 2 = 26)
Далее мы видим, что у нас есть связь числа с 10.У нас 2 м и 8 м.
Сначала мы можем сложить эти две стороны вместе.
8 + 2 = 10
Десять — это число, с которым проще работать и добавлять. Добавление десяти просто означает добавление еще одного к нашему столбцу десятков. Мы пытаемся найти пары сторон, которые добавят десять, если сможем.
Теперь добавляем последнюю сторону, 9 м.
26 + 10 + 9 = 45
Самый простой способ сделать это вычисление: 10 + 9 равно 19, а прибавление 19 равнозначно сложению 20 с последующим вычитанием 1.
Этот метод известен как стратегия сложения путем компенсации. Чтобы узнать больше об этом, см. Наш урок: Добавление с помощью стратегии компенсации.
26 + 10 + 9 то же самое, что 26 + 19, то же самое, что 26 + 20, затем вычтите 1.
26 + 20 = 46, а затем мы вычитаем единицу для компенсации и получаем 45, как и раньше.
Периметр этого неправильного пятиугольника составляет 45 м .
Метод определения периметра, как правило, одинаков для всех наших неправильных форм.Мы перемещаемся по внешней стороне нашей формы и складываем внешние края, скрещивая их по мере добавления.
Помните, что если есть несколько сторон одинаковой длины, можно использовать умножение вместо их сложения. Мы также можем искать кратные десяти и числовые связи, чтобы помочь в нашем добавлении, наряду со стратегией сложения с компенсацией, если нам нужно добавить число, такое как 9 или 19.
Периметр прямоугольника — Веб-формулы

В прямоугольнике расстояние вокруг внешней стороны прямоугольника называется периметром.Прямоугольник двумерный; однако периметр является одномерным и измеряется в линейных единицах, таких как футы, метры и т. д.
Периметр прямоугольника — это общая длина всех четырех сторон.
Периметр прямоугольника = 2L + 2W.
Пример 1: Прямоугольник имеет длину 13 см и ширину 8 см. решить для периметра прямоугольника.
Решение :
Учитывая, что:
Длина (l) = 13 см
Ширина (w) = 8 см
Периметр прямоугольника = 2 (l + w) единиц
P = 2 (13 + 8)
P = 2 (21)
P = 42
Таким образом, периметр прямоугольника равен 42 см.
Пример 2: Если длина прямоугольника равна 2x + 1, а ширина — 2x — 1. Если его площадь составляет 15 см ², каковы размеры прямоугольника и каков его периметр?
Решение :
Мы знаем, что размеры прямоугольника в единицах x:
l = 2x + 1
w = 2x — 1
Поскольку площадь прямоугольника определяется как:
A = l * w
Мы можем подставить выражения для длины и ширины в уравнение для площади, чтобы определить значение x.
A = l * w
15 = (2x + 1) (2x -1)
15 = 4x ² — 1
16 = 4x ²
x = ± 2

Обратите внимание, что значение x должно быть положительным, и поэтому в нашем случае значение x равно 2. И теперь мы имеем:
l = 5 см
w = 3 см
Следовательно, размеры составляют 5 см и 3 см. .
Теперь, подставив эти значения в формулу для периметра, мы получим
Пример 3: Найдите площадь и периметр прямоугольника длиной 24 м и шириной 12 м?
Решение :
Учитывая, что:
длина = L = 24 м
ширина = W = 12 м
Пример 4: Найдите площадь и периметр прямоугольника шириной 4 см и высотой 3 см.
Решение :
Площадь = b × h = 4 × 3 = 12 см ².
Периметр = 2 (b) + 2 (h) = 2 (4) + 2 (3) = 8 + 6 = 14.
Пример 5: Вычислите периметр прямоугольника длиной 18 см и ширина 7см
Раствор :
Учитывая, что:
L = 18 см
B = 7 см
Пример 6: Найдите периметр прямоугольника, длина которого составляет 6 дюймов, а ширина — 4 дюйма.
Решение :
P = 2 (L + B)
P = 2 (6 + 4)
P = 20 дюймов
Пример 7: Мальчик 5 раз ходит по парку. Если размер парка 100 на 50 метров, найдите расстояние, которое прошел мальчик. Если он пройдет 100 метров за 5 минут, сколько всего у него на это уйдет?
Решение :
При этом:
Длина = L = 100 м
Ширина = W = 50 м
Раундов = 5
Время на 100м = 5 минут.
Периметр парка:
P = 2 L + 2 W.
Р = 2 × 100 + 2 × 50
Р = 200 + 100
P = 300 м
Общее пройденное расстояние = 5 × Периметр парка.
No related posts.